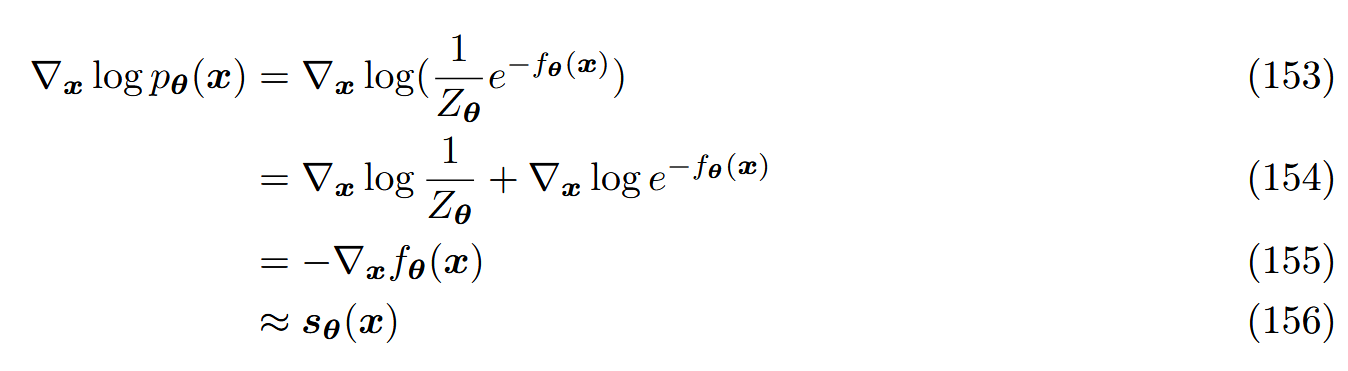基于分数的生成模型

基于分数的生成模型

基于能量的模型

任意分布都可以被写为：

pθ(x)=1Zθe−fθ(x)(152)p_\theta(x)=\frac{1}{Z_\theta}e^{-f_\theta(x)}\tag{152}

fθ(x)f_\theta(x) 是一个任意的、参数化的函数——能量函数，通常被建模为一个NN，ZθZ_\theta 是正则化常数使得 ∫pθ(x)dx=1\int p_\theta(x)dx=1 ,如果使用最大似然估计，对复杂的 fθ(x)f_\theta(x) 来说，ZθZ_\theta 可能难以处理

分数模型

上面的问题可以使用一个NN sθ(x)s_\theta(x) 来学习 p(x)p(x) 的分数函数 ∇log⁡p(x)\nabla\log p(x) 所避免。动机：

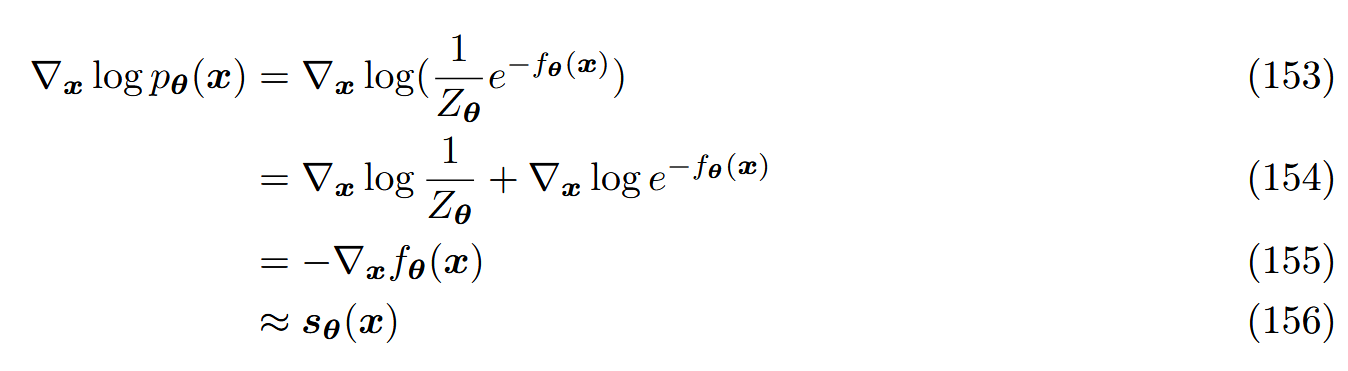
因此不需要表示任何正则化常数，分数模型可以通过最小化Fisher散度来优化：

Ep(x)[∥sθ(x)−∇log⁡p(x)∥22](157)\mathbb E_{p(x)}\Big[\left\|s_\theta(x)-\nabla\log p(x)\right\|_2^2\Big]\tag{157}

对于每个 xx 来说，它的对数似然的梯度根本上描述了在数据空间中进一步增加它的对数似然的方向。直觉上，分数函数在数据 x 所在的整个空间上定义了一个向量场，指向众数：

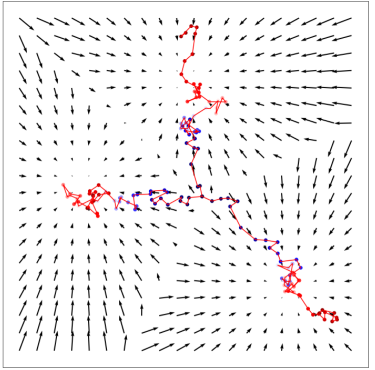
通过学习真实数据分布的分数函数，我们可以从相同空间中的任一点开始，逐渐地跟随分数直到模式到达来生成样本。采样过程为已知的郎之万采样：

xi+1←xi+c∇log⁡p(xi)+2cϵ, i=0,1,...,K(158)x_{i+1}\gets x_i+c\nabla\log p(x_i)+\sqrt{2c}\epsilon,\ i=0,1,...,K\tag{158}

x0x_0 是从先验分布中随机采样，ϵ∼N(ϵ;0,I)\epsilon\sim\mathcal N(\epsilon;\mathbf 0,\mathbf I) 是一个额外的噪声项用来保证生成样本不总是崩溃到一个模式，而是为了多样性环绕在它周围，保留一定的随机性。由于ground-truth分数函数对于复杂分布的自然图像来说不可获取，于是使用分数匹配方法来解决。

普通分数匹配存在三个问题：

  1. 当 xx 在高维空间的低维流形上时，分数函数是不明确的。所有不在低维流形的点的概率为0，此时对数没有定义，而自然图像通常在整个环境空间的低维流形上

  2. 通过普通分数匹配训练的分数函数在低密度区域可能是不正确的，因为我们最小化的目标是关于 p(x)p(x) 的期望，从它的样本中训练，模型无法接收到很少见或者看不到的样本的正确的学习信号。（采样策略是高维空间的随机位置开始，很可能是随机噪声）

  3. 郎之万动力采样可能不会拟合，即使使用ground-truth分数：

    假设真实数据分布是两个不相交的分布的混合

    p(x)=c1p1(x)+c2p2(x)(159) p(x)=c_1p_1(x)+c_2p_2(x)\tag{159}

    在计算分数时，它们的混合系数被丢掉，那么从它们中间的初始点使用郎之万动力学采样的话，到达它们每个模式的机会都是粗略相等的，尽管可能某一个分布的权重更大

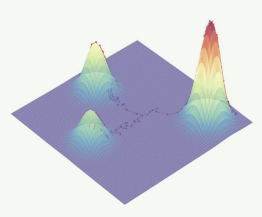
    解决方案：在数据中加入多个水平的高斯噪声(去噪分数匹配)

    1. 由于高斯噪声的假设是整个空间，于是扰动后的数据不再局限于低维流形
    2. 加入较大的高斯噪声将增大每种模式在数据分布中覆盖的面积，在低密度区域增加了更多训练信号
    3. 加入多个水平的高斯噪声并增加方差将使得结果的中间分布尊重ground-truth的混合系数

    于是，形式上，选择正的噪声水平序列 {σt}t=1T\{\sigma_t\}_{t=1}^T ，以及定义一个逐渐扰动数据分布的序列：

    pσt(xt)=∫p(x)N(xt;x,σt2I)dx(160)p_{\sigma_t}(x_t)=\int p(x)\mathcal N(x_t;x,\sigma_t^2\mathbf I)dx\tag{160}

    sθ(x,t)s_\theta(x,t) 使用分数匹配训练学习同时所有噪声水平的分数函数：

    arg minθ∑t=1Tλ(t)Epσt(xt)[∥sθ(x,t)−∇log⁡pσt(xt)∥22](161)\underset{\theta}{arg\ min}\sum_{t=1}^T\lambda(t)\mathbb E_{p_{\sigma_t}(x_t)}\Big[\left\|s_\theta(x,t)-\nabla\log p_{\sigma_t}(x_t)\right\|_2^2\Big]\tag{161}

λ(t)\lambda(t) 是正的权重函数，通常被选择为 λ(i)=σi2\lambda(i)=\sigma_i^2 由于噪声水平随着时间稳定下降，因此要随着时间减少步长，使得样本最后集中在真实的模式上。

∇xtlog⁡pσt(xt)=∇xtlog⁡pσt(xt∣x)p(x)=∇xtlog⁡pσt(xt∣x)(162)\nabla_{x_t}\log p_{\sigma_t}(x_t)=\nabla_{x_t}\log p_{\sigma_t}(x_t|x)p(x)=\nabla_{x_t}\log p_{\sigma_t}(x_t|x)\tag{162}

∇xtlog⁡pσt(xt∣x)=∇xtlog⁡{12πσtexp⁡(−(xt−x)22σt2)}=∇xt[−(xt−x)22σt2]=−xt−xσt2=−ϵσt(163)\nabla_{x_t}\log p_{\sigma_t}(x_t|x)=\nabla_{x_t}\log \Big\{\frac{1}{\sqrt{2\pi}\sigma_t}\exp\Big(-\frac{(x_t-x)^2}{2\sigma_t^2}\Big)\Big\}\\ =\nabla_{x_t}\Big[-\frac{(x_t-x)^2}{2\sigma_t^2}\Big]\\ =-\frac{x_t-x}{\sigma_t^2}\\ =-\frac{\epsilon}{\sigma_t}\tag{163}

于是优化目标可以写为：

arg minθ∑t=1Tλ(t)Epσt(xt)[∥sθ(x,t)+xt−xσt2∥22]=arg minθ∑t=1TEpσt(xt)[∥σtsθ(x,t)+ϵ∥22](164)\underset{\theta}{arg\ min}\sum_{t=1}^{T}\lambda(t)\mathbb E_{p_{\sigma_t}(x_t)}\Bigg[\left\|s_\theta(x,t)+\frac{x_t-x}{\sigma_t^2}\right\|_2^2\Bigg]\\ =\underset{\theta}{arg\ min}\sum_{t=1}^{T}\mathbb E_{p_{\sigma_t}(x_t)}\Big[\left\|\sigma_ts_\theta(x,t)+\epsilon\right\|_2^2\Big]\tag{164}

SDE推导

众所周知，扩散模型中 x0→xT,xT→x0x_0\to x_T,x_T\to x_0 的过程一种随机过程，于是考虑使用随机微分方程（Stochastic Differential Equations，SDE）来刻画。

原始扩散过程为离散形式，使用SDE进行连续的描述，于是前向扩散过程可以看作一个伊藤扩散过程的解：

dx=f(x,t)dx+g(t)dωdx=f(x,t)dx+g(t)d\omega

其中：

dx=lim⁡Δt→0(xt+Δt−xt)dx=\lim\limits_{\Delta t\to0}(x_{t+\Delta t}-x_t)

因此原来离散形式的 xt→xt+1x_t\to x_{t+1} 就变为连续形式的 xt→xt+Δtx_{t}\to x_{t+\Delta t} ，于是：

xt+Δt=xt+f(x,t)Δt确定部分+g(t)Δtϵ随机部分,ϵ∼N(0,I)x_{t+\Delta t}=x_t+\underset{确定部分}{f(x,t)\Delta t}+\underset{随机部分}{g(t)\sqrt{\Delta t}\epsilon},\epsilon\sim\mathcal N(0,I)

原来离散的前向过程：x0→x1→x2→...→xTx_0\to x_1\to x_2\to ...\to x_T ，现在连续的前向过程：x0→xΔt→x2Δt→...→xTx_0\to x_{\Delta t}\to x_{2\Delta t}\to ... \to x_T

有了前向过程的SDE后，需要分析反向过程以还原真实分布，

p(xt+Δt∣xt)=N(xt+Δt;xt+f(x,t)Δt,g2(t)ΔtI)∝exp⁡(∥xt+Δt−xt−f(x,t)Δt∥22g2(t)Δt)p(x_{t+\Delta t}|x_t)=\mathcal N(x_{t+\Delta t};x_t+f(x,t)\Delta t,g^2(t)\Delta tI)\\ \propto\exp(\frac{\left\|x_{t+\Delta t}-x_t-f(x,t)\Delta t\right\|^2}{2g^2(t)\Delta t})

根据贝叶斯规则：

p(xt∣xt+Δt)=p(xt+Δt∣xt)p(xt)p(xt+Δt)=p(xt+Δt∣xt)exp⁡(log⁡p(xt)−log⁡p(xt+Δt))=exp⁡(−∥xt+Δt−xt−f(x,t)Δt∥22g2(t)Δt+log⁡p(xt)−log⁡p(xt+Δt))p(x_t|x_{t+\Delta t})=\frac{p(x_{t+\Delta t}|x_t)p(x_t)}{p(x_{t+\Delta t})}\\ =p(x_{t+\Delta t}|x_t)\exp(\log p(x_t)-\log p(x_{t+\Delta t}))\\ =\exp(-\frac{\left\|x_{t+\Delta t}-x_t-f(x,t)\Delta t\right\|^2}{2g^2(t)\Delta t}+\log p(x_t)-\log p(x_{t+\Delta t}))

对 log⁡p(xt+Δt)\log p(x_{t+\Delta t}) 进行泰勒展开：

log⁡p(xt+Δt)≈log⁡p(xt)+(xt+Δt−xt)∇xtlog⁡p(xt)+Δt∂log⁡p(xt)∂t\log p(x_{t+\Delta t})\approx \log p(x_t)+(x_{t+\Delta t}-x_t)\nabla_{x_t}\log p(x_t)+\Delta t\frac{\partial \log p(x_t)}{\partial t}

代入得：

p(xt∣xt+Δt)∝exp⁡(−∥xt+Δt−xt−f(x,t)Δt∥22g2(t)Δt+(xt+Δt−xt)∇xtlog⁡p(xt)−Δt∂log⁡p(xt)∂t)=exp⁡(−∥xt+Δt−xt−[f(x,t)−g2(t)∇xtlog⁡p(xt)]Δt∥22g2(t)Δt+Ot)p(x_t|x_{t+\Delta t})\propto \exp(-\frac{\left\|x_{t+\Delta t}-x_t-f(x,t)\Delta t\right\|^2}{2g^2(t)\Delta t}+(x_{t+\Delta t}-x_t)\nabla_{x_t}\log p(x_t)-\Delta t\frac{\partial \log p(x_t)}{\partial t})\\ =\exp(-\frac{\left\|x_{t+\Delta t}-x_t-[f(x,t)-g^2(t)\nabla_{x_t}\log p(x_t)]\Delta t\right\|^2}{2g^2(t)\Delta t}+\mathscr Ot)

当 Δt→0\Delta t\to0 时，Ot→0\mathscr Ot\to0 ，于是：

p(xt∣xt+Δt)∝exp⁡(−∥xt+Δt−xt−[f(x,t)−g2(t)∇xtlog⁡p(xt)]Δt∥22g2(t)Δt)≈exp⁡(−∥xt−xt+Δt+[f(x,t+Δt)−g2(t+Δt)∇xt+Δtlog⁡p(xt+Δt)]Δt∥22g2(t+Δt)Δt)p(x_t|x_{t+\Delta t})\propto \exp(-\frac{\left\|x_{t+\Delta t}-x_t-[f(x,t)-g^2(t)\nabla_{x_t}\log p(x_t)]\Delta t\right\|^2}{2g^2(t)\Delta t})\\ \approx \exp(-\frac{\left\|x_t-x_{t+\Delta t}+[f(x,t+\Delta t)-g^2(t+\Delta t)\nabla_{x_{t+\Delta t}}\log p(x_{t+\Delta t})]\Delta t\right\|^2}{2g^2(t+\Delta t)\Delta t})

因此：

p(xt∣xt+Δt)=N(xt;xt+Δt−[f(x,t+Δt)−g2(t+Δt)∇xt+Δtlog⁡p(xt+Δt)]Δt,g2(t+Δt)ΔtI)p(x_t|x_{t+\Delta t})=\mathcal N(x_t;x_{t+\Delta t}-[f(x,t+\Delta t)-g^2(t+\Delta t)\nabla_{x_{t+\Delta t}}\log p(x_{t+\Delta t})]\Delta t,g^2(t+\Delta t)\Delta tI)

取 Δt→0\Delta t\to0 ，以及 dx=lim⁡Δt→0(xt+Δt−xt)dx=\lim\limits_{\Delta t\to0}(x_{t+\Delta t}-x_t) 得最后的reverse-time SDE：

dx=[f(x,t)−g2(t)∇xlog⁡pt(x)]dt+g(t)dωdx=[f(x,t)-g^2(t)\nabla_x\log p_t(x)]dt+g(t)d\omega

VE-SDE vs. VP-SDE

将NCSN以及DDPM均考虑到SDE框架中，分别为Variance Exploding(VE) SDE和Variance Preserving(VP) SDE。

VE-SDE

对于NCSN，扩散公式为：

xT=x0+σTεx_T=x_0+\sigma_T\varepsilon

依靠非常大的 σT\sigma_T 使得 xTx_T 变为以 ϵ\epsilon 主导的高斯噪声，因此是Variance Exploding（方差爆炸）。

NCSN每一步的扰动核 pσi(x∣x0)p_{\sigma_i}(x|x_0) 的马尔科夫链表示：

xi=xi−1+σi2−σi−12zi−1,i=1,...,Nx_i=x_{i-1}+\sqrt{\sigma_i^2-\sigma_{i-1}^2}z_{i-1},i=1,...,N

这里的 zi−1∼N(0,I)z_{i-1}\sim\mathcal N(0,I) ,当 N→∞N\to\infty 时，马尔科夫链 {xi}i=1N\{x_i\}_{i=1}^N 就变成了连续的随机过程 {x(t)}t=01\{x(t)\}_{t=0}^1 ,{σi}i=1N\{\sigma_i\}_{i=1}^N 变为函数 σ(t)\sigma(t) , ziz_i 变为 z(t)z(t) , 这里的连续时间变量 t∈[0,1]t\in [0,1] , 而不是整数 i∈{1,2,...,N}i\in \{1,2,...,N\}. 令 x(iN)=xi,σ(iN)=σi,z(iN)=zix(\frac{i}{N})=x_i,\sigma(\frac{i}{N})=\sigma_i,z(\frac{i}{N})=z_i , 于是 Δt=1N,t∈{0,1N,...,N−1N}\Delta t=\frac1N,t\in\{0,\frac1N,...,\frac{N-1}{N}\} :

x(t+Δt)=x(t)+σ2(t+Δt)−σ2(t)z(t)=x(t+σ2(t+Δt)2−σ2(t)ΔtΔtz(t)=x(t)+Δσ2ΔtΔtz(t)x(t+\Delta t)=x(t)+\sqrt{\sigma^2(t+\Delta t)-\sigma^2(t)}z(t)\\ =x(t+\sqrt{\frac{\sigma^2(t+\Delta t)^2-\sigma^2(t)}{\Delta t}}\sqrt{\Delta t}z(t)\\ =x(t)+\sqrt{\frac{\Delta\sigma^2}{\Delta t}}\sqrt{\Delta t}z(t)

于是当 Δt→0\Delta t\to0 时：

f(x,t)=0,g(t)=d(σt2)dtf(x,t)=0,g(t)=\sqrt{\frac{d(\sigma_t^2)}{dt}}

于是VE-SDE为：

dx=d(σt2)dtdωdx=\sqrt{\frac{d(\sigma_t^2)}{dt}}d\omega

VP-SDE

对于DDPM，扩散公式为：

xT=αˉTx0+1−αˉTεx_T=\sqrt{\bar\alpha_T}x_0+\sqrt{1-\bar\alpha_T}\varepsilon

依靠非常小的 αˉT\sqrt{\bar\alpha_T} 去压制 x0x_0 ，而本身方差 1−αˉT\sqrt{1-\bar\alpha_T} 并不大，因此是Variance Preserving（方差缩紧）。

DDPM的扰动核 {pαi(x∣x0)}i=1N\{p_{\alpha_i}(x|x_0)\}_{i=1}^N , 它的离散化的马尔科夫链表示：

xi=1−βixi−1+βizi−1,i=1,2,...,Nx_i=\sqrt{1-\beta_i}x_{i-1}+\sqrt{\beta_i}z_{i-1},i=1,2,...,N

这里 zi−1∼N(0,I)z_{i-1}\sim\mathcal N(0,I) , 为了获得当 n→∞n\to \infty 时的马尔科夫链的极限，定义一个噪声的辅助集合 {βˉi=Nβi}i=1N\{\bar\beta_i=N\beta_i\}_{i=1}^N ,于是：

xi=1−βˉiNxi−1+βˉiNzi−1,i=1,2,...,Nx_i=\sqrt{1-\frac{\bar\beta_i}{N}}x_{i-1}+\sqrt{\frac{\bar\beta_i}{N}}z_{i-1},i=1,2,...,N

当 N→∞N\to \infty 时，同上，得：

x(t+Δt)=1−β(t+Δt)Δt x(t)+β(t+Δt)Δt z(t)≈(1−12β(t+Δt)Δt)x(t)+β(t+Δt)Δt z(t)≈(1−12β(t)Δt)x(t)+β(t)Δt z(t)x(t+\Delta t)=\sqrt{1-\beta(t+\Delta t)\Delta t}\ x(t)+\sqrt{\beta(t+\Delta t)\Delta t}\ z(t)\\ \approx (1-\frac12\beta(t+\Delta t)\Delta t)x(t)+\sqrt{\beta(t+\Delta t)\Delta t}\ z(t)\\ \approx (1-\frac12\beta(t)\Delta t)x(t)+\sqrt{\beta(t)\Delta t}\ z(t)

于是当 Δt→0\Delta t\to 0 时：

f(x,t)=−12β(t)x(t),g(t)=β(t)f(x,t)=-\frac12\beta(t)x(t),g(t)=\sqrt{\beta(t)}

于是VP-SDE为：

dx=−12β(t)xdt+β(t)dωdx=-\frac12\beta(t)xdt+\sqrt{\beta(t)}d\omega

#Diffusion
基于分数的生成模型
https://summerwrain.github.io/2023/11/12/Understanding diffusion基于分数的模型/
作者
SummerRain
发布于
2023年11月12日
许可协议