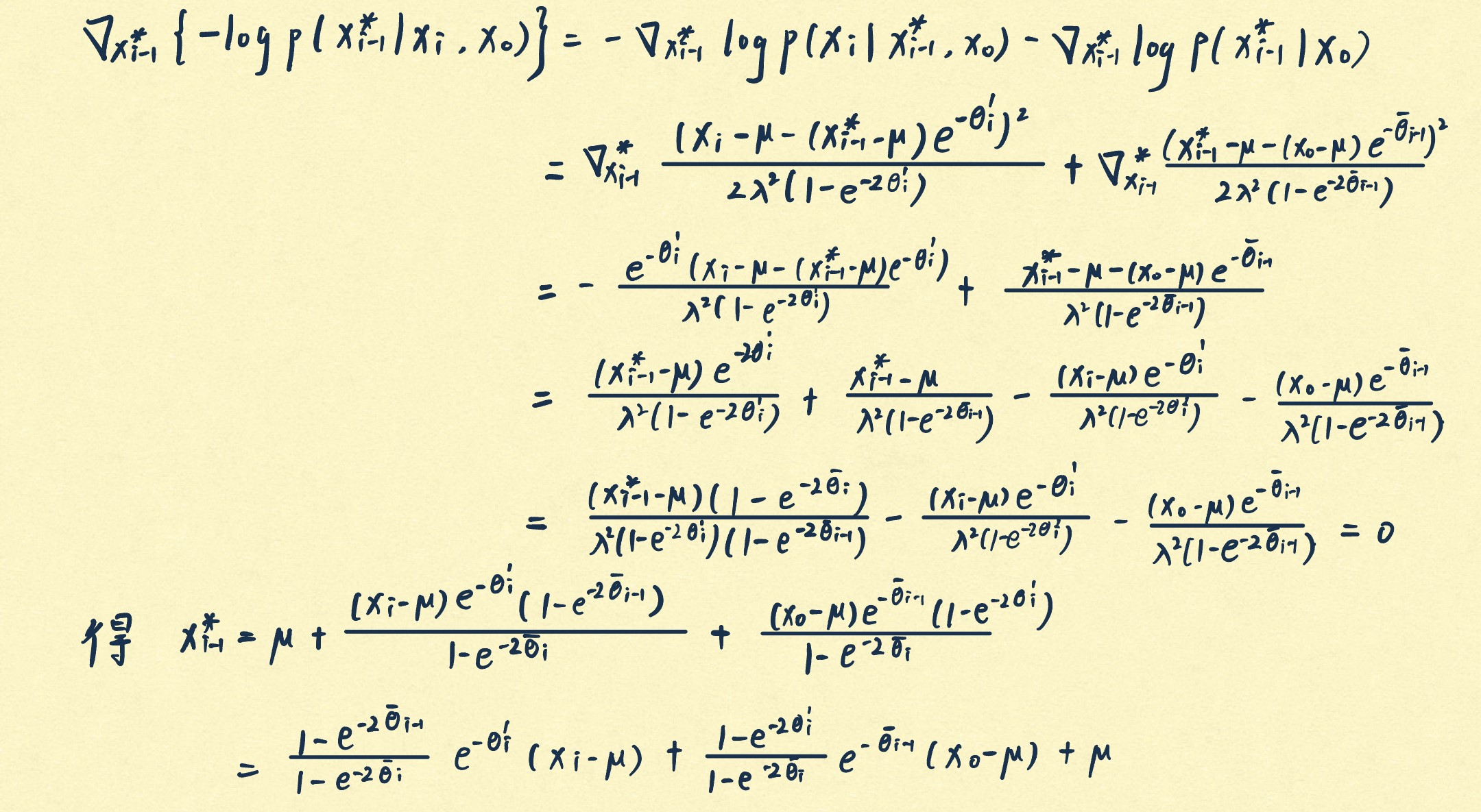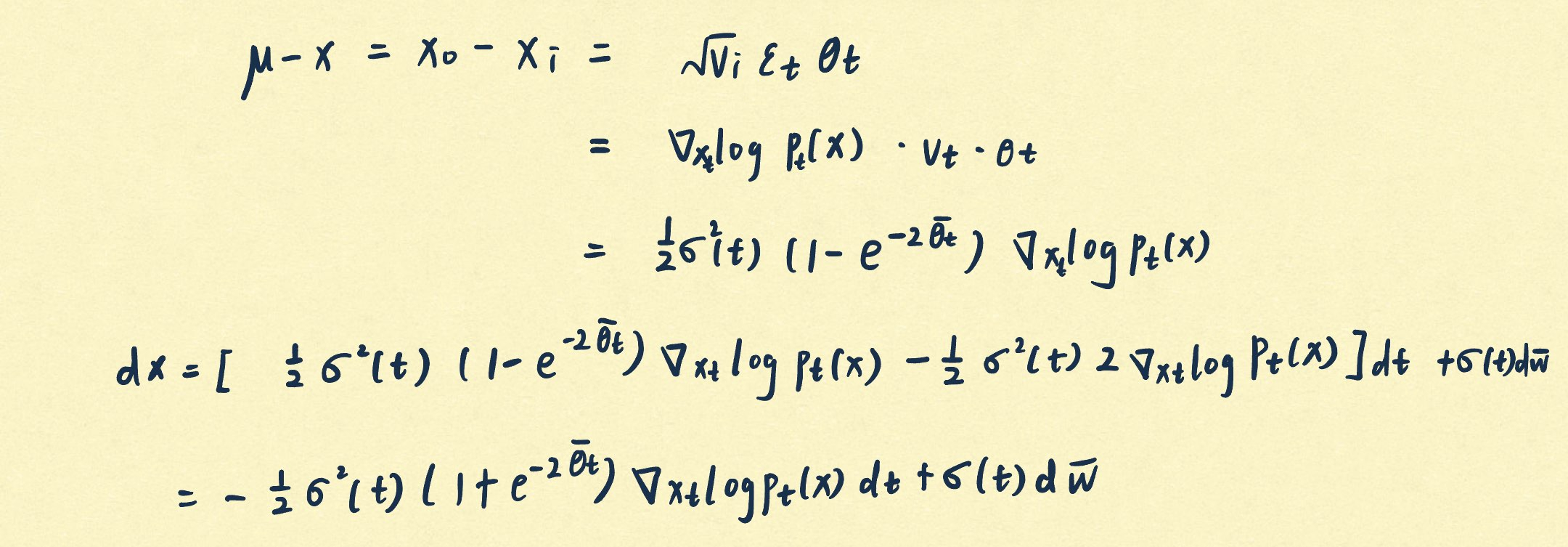IR-SDE

Image Restoration with Mean-Reverting Stochastic Differential Equations

背景

以往的方法的反向过程会初始化一个较高方差的噪声，可能会导致ground-truth高质量图像的恢复效果不好，虽然可以获得较高的感知分数，但是往往会在基于像素或结构的退化标准方面表现不太满意。

贡献

为一般的IR问题提出一种SDE方法。mean-recerting SDE关键思想：将高质量的图像转换为退化图像，作为具有固定高斯噪声的均值状态，然后去估计reverse-time SDE，不需要有任何task-specific的先验知识。提出了最大似然目标学习优化的reverse轨迹。

方法

前向过程

$$dx=\theta_t(\mu-x)dt+\sigma_tdw$$

$\mu$ 为状态均值，$\theta_t,\sigma_t$ 是与时间相关的正参数，分别表征了均值恢复和随机波动的速度。$\mu$ 与 $x(0)$ 分别为退化的LQ图像和ground-truth的HQ图像对。由于$\mu$ 依赖于$x(0)$ ，$x(0)$ 与布朗运动无关，因此该SDE在伊藤形式上依然有效。
令$\sigma_t^2/\theta_t=2\lambda^2$ ，$\lambda^2$ 为固定的方差。给定任意的 $x(s),s<t$ ，SDE的解为:

$$x(t)=\mu+(x(s)-\mu)e^{-\bar\theta_{s:t}}+\int_s^t\sigma_ze^{-\bar\theta_{z:t}}dw(z)$$

$\bar\theta_{s:t}:=\int_s^t\theta_zdz$ 已知，则中间的转移步 $p(x(t)|x(s))=\mathcal N(x(t)|m_{s:t}(x(s)),v_{s:t})$ ：

$$m_{s:t}(x(s)):=\mu+(x(s)-\mu)e^{-\bar\theta_{s:t}},\\ v_{s:t}:=\int_s^t\sigma_z^2e^{-2\bar\theta_{z:t}}dz\\ =\lambda^2(1-e^{-2\bar\theta_{s:t}})$$

证明：

需求解的SDE：

$$\mathrm dx=\theta_t(\mu-x)\mathrm dt+\sigma_t \mathrm dw$$

为简便，使用 $\bar\theta_t$ 替换 $\bar\theta_{0:t}$ ，定义一个代理可微函数(方便求解)：

$$\psi(x,t)=x\mathrm e^{\bar\theta_t}$$

根据伊藤公式：

$$\mathrm d\psi(x,t)=\frac{\partial\psi}{\partial t}(x,t)\mathrm dt+\frac{\partial\psi}{\partial x}(x,t)\mathbf f(x,t)\mathrm dt\\ +\frac12\frac{\partial^2\psi}{\partial x^2}(x,t)g(t)^2\mathrm dt\\ +\frac{\partial\psi}{\partial x}(x,t)g(t)\mathrm {dw_t}$$

将式 $(4)$ 代入 $(6)$ 得:

$$\mathrm d\psi(x,t)=\mu\theta_t\mathrm e^{\bar\theta_t}\mathrm dt+\sigma_t\mathrm e^{\bar\theta_t}\mathrm{dw}_t$$

积分得：

$$\psi(x,t)-\psi(x,s)=\int_s^t\mu\theta_z\mathrm e^{\bar\theta_z}\mathrm dz+\int_s^t\sigma_z\mathrm e^{\bar\theta_z}\mathrm{dw}(z)$$

在这里，$\int_s^t\sigma_z\mathrm e^{\bar\theta_z}\mathrm{dw}(z)\sim\mathcal N(0,\int_s^t\sigma^2_z\mathrm e^{2\bar\theta_z}dz)$

证明：

$$Var(\int_s^tH_zdW(z))\approx Var(\sum_{i=1}^NH_{t_i}(W_{t_i}-W_{t_{i-1}}))\\ =\sum_{i=1}^NVar(H_{t_i}(W_{t_i}-W_{t_{i-1}}))\\ =\sum_{i=1}^NH_{t_i}^2Var(W_{t_i}-W_{t_{i-1}})\\ =\sum_{i=1}^NH_{t_i}^2(t_i-t_{i-1})$$

$$\lim_{max \Delta t_i\to0}\sum_{i=1}^NH_{t_i}^2(t_i-t_{i-1})=\int_s^tH_z^2dz$$

由于 $\mathrm d\bar\theta_t=\mathrm d\int_0^t\theta_z\mathrm dz=\theta_t$ ,于是：

$$x(t)\mathrm e^{\bar\theta_t}-x(s)\mathrm e^{\bar\theta_s}=\mu(\mathrm e^{\bar\theta_t}-\mathrm e^{\bar\theta_s})+\int_s^t\sigma_z\mathrm e^{\bar\theta_z}\mathrm{dw}(z)$$

两边同时除以 $\mathrm e^{\bar\theta_t}$ 得：

$$x(t)=\mu+(x(s)-\mu)\mathrm e^{-\bar\theta_{s:t}}+\int_s^t\sigma_z\mathrm e^{-\bar\theta_{z:t}}\mathrm {dw}_z$$

$$\int_s^t\sigma_z^2\mathrm e^{-2\bar\theta_{z:t}}\mathrm dz=\frac{\sigma_t^2}{2\theta_t}e^0-\frac{\sigma^2_s}{2\theta_s}\mathrm e^{-2\bar\theta_{s:t}}=\lambda^2(1-\mathrm e^{-2\bar\theta_{s:t}})$$

证毕

当 $t\to\infty$ 时，$m_t$ 趋于LQ图像 $\mu$ ，$v_t$ 趋于 $\lambda^2$ ，即SDE将HQ图像扩散到LQ图像加一张固定高斯噪声。

反向过程

$$\mathrm dx=[\theta_t(\mu-x)-\sigma^2_t\nabla_x\log p_t(x)]dt+\sigma_t\mathrm d\hat w$$

每一步的ground-truth score:

$$\nabla_x\log p_t(x|x(0))=-\frac{x(t)-m_t(x)}{v_t}$$

重新参数化 $x(t)=m_t(x)+\sqrt{v_t}\epsilon_t,\epsilon\sim\mathcal n(0,I)$ ,于是：

$$\nabla_x\log p_t(x|x(0))=-\frac{\epsilon_t}{\sqrt v_t}$$

训练噪声估计网络 $\tilde\epsilon_\phi(x(t),\mu,t)$ :

$$L_\gamma(\phi):=\sum_{i=1}^{T}\gamma_i\mathbb E[\left\|\tilde\epsilon_\phi(x(t),\mu,t)-\epsilon_i\right\|]$$

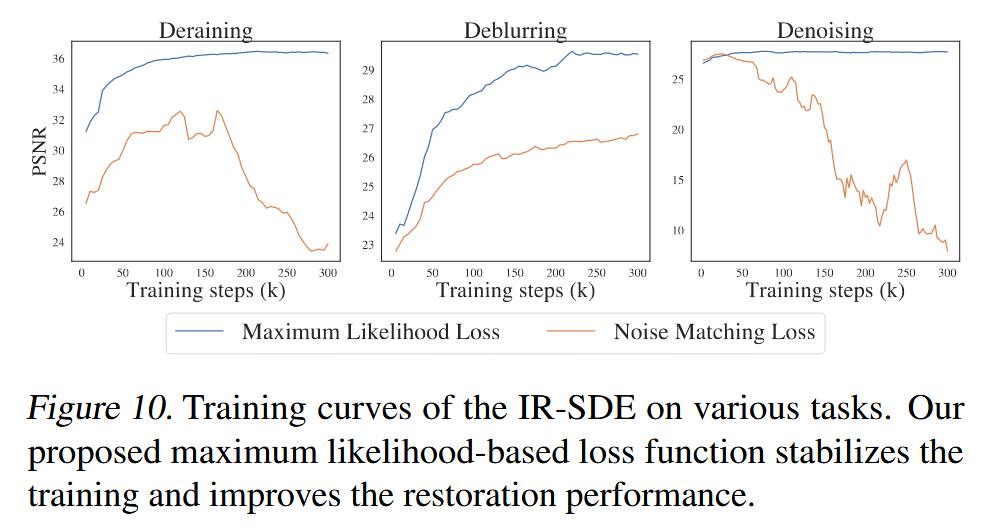
上式虽然比较简单，但是往往应用到复杂退化场景时会不稳定。原因：试图学习给定时间的瞬时噪声。

解决方法： 提出最大似然目标尝试寻找给定 $x_0$ 后 $x_{1:T}$ 的最优轨迹（而不是更准确的分数函数）

最大似然目标：

$$p(x_{1:T}|x_0)=p(x_T|x_0)\prod_{i=2}^Tp(x_{i-1}|x_i,x_0)$$

于是最佳反向状态为最小化负的对数似然：

$$x_{i-1}^*=\underset{x_{i-1}}{\mathrm{arg\ min}}[-\log p(x_{i-1}|x_i,x_0)]$$

令 $\theta'_i:=\int_{i-1}^i\theta_t\mathrm dt$ ,通过求解可得最优轨迹：

$$x_{i-1}^*=\frac{1-\mathrm e^{-2\bar\theta_{i-1}}}{1-\mathrm e^{-2\bar\theta_i}}\mathrm e^{-\theta'_i}(x_i-\mu)\\ +\frac{1-\mathrm e^{-2\theta_i'}}{1-\mathrm e^{\bar\theta_i}}(x_0-\mu)+\mu$$

证明：

根据贝叶斯规则

$$-\log p(x_{i-1}|x_i,x_0)=-\log\frac{p(x_i|x_{i-1},x_0)p(x_{i-1}|x_0)}{p(x_i|x_0)}\\ \propto -\log p(x_i|x_{i-1},x_0)-\log p(x_{i-1}|x_0)$$

令负的对数似然的梯度为0：

证毕，二阶导数为正，因此 $x_{i-1}^*$ 确实为最优点

训练噪声估计网络 $\tilde\epsilon_\phi(x_i,\mu,i)$ :

$$J_\gamma(\phi):=\sum_{i=1}^T\gamma_i\mathbb E[\left\|x_i-(dx_i)_{\tilde\epsilon_\phi}-x_{i-1}^*\right\|]$$

$(dx_i)_{\tilde\epsilon_\phi}$ 为式 $(14)$ 的反向SDE，其中分数由 $\tilde\epsilon_\phi$ 估计，由于扩散项的期望为0，于是只需要考虑漂移项。

实验

Deraining

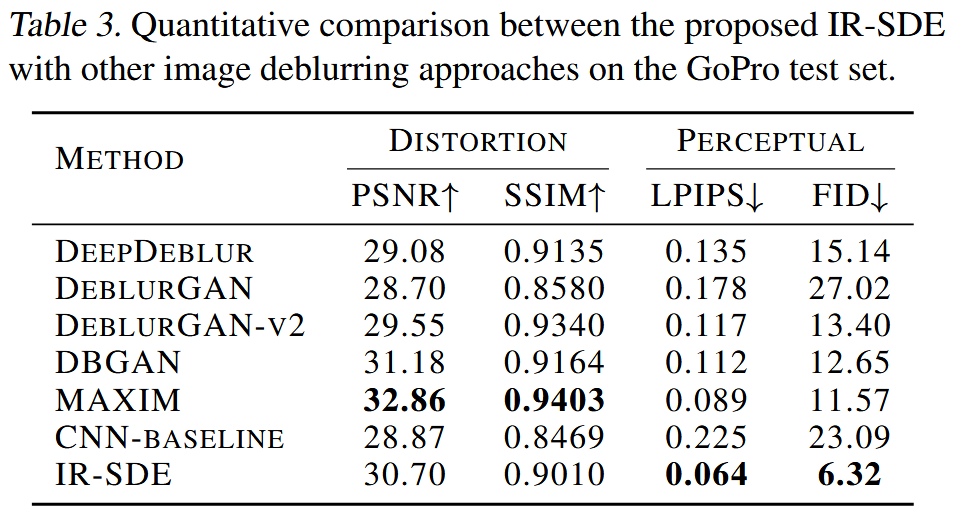
Debluring

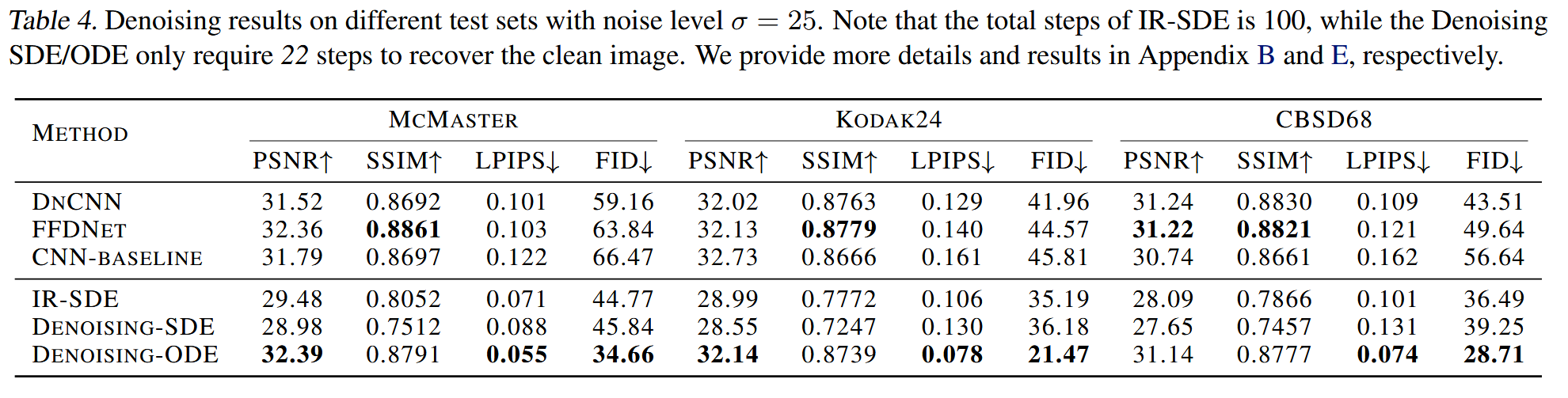
Gaussian Image Denoising

提出Denoising-SDE：将干净图像设为均值 $\mu=x_0$ ，可以以更少的时间步进行去噪。因此可以将任意噪声图作为中间状态，将其直接反转为干净图像。

提出Denoising-ODE：由于只有高斯噪声，因此可以直接使用ODE，没有额外的噪声直接去噪：

$$\mathrm dx=[\theta_t(\mu-x)-\sigma^2_t\nabla_x\log p_t(x)]dt$$

$$p_{noise}(x_i|x_0)=\mathcal N(m_i(x_0),v_i)$$

这里的 $m_i(x_0)=x_0,v_i=\lambda^2(1-e^{-2\bar\theta_i})$ ，最优轨迹变为：

$$x_{i-1}^*=\frac{1-\mathrm e^{-2\bar\theta_{i-1}}}{1-\mathrm e^{-2\bar\theta_i}}\mathrm e^{-\theta'_i}(x_i-x_0)+x_0$$

$$x_i=m_i+\sqrt{v_i}\epsilon_t,\epsilon\sim\mathcal N(0,I)$$

将式 $(26)$ 代入式 $(14)$ 得Denoising-SDE:

对应的ODE：

$$dx=-\frac12\sigma_t^2\mathrm e^{-2\bar\theta_t}\nabla_{x_t}\log p_t(x)dt$$

一旦知道真实噪声水平 $\sigma_{real}$ 则可以直接推出相应的 $t^*$ 使得 $p_{noise}(x_i|x_0)$ 的方差刚好为噪声水平：

$$\sigma_{real}^2=v_t=\lambda^2(1-\mathrm e^{-2\bar\theta_t})$$

于是：

$$t^*=\underset{t}{arg\ min}\left\|\bar\theta_t-\frac1{2\Delta t}\log (1-\frac{\sigma_{real}^2}{\lambda^2 })\right\|$$

局限与未来方向

$v_t$ 中的指数项会使得在最后几步的方差变得过于平滑，使得相邻状态很相似，使得学习变得困难。解决方案：改进 $\theta$ 时间表。

采样步骤的优化，以减少计算成本

参考

[1] Z. Luo, F. K. Gustafsson, Z. Zhao, J. Sjölund, and T. B. Schön, “Image Restoration with Mean-Reverting Stochastic Differential Equations.” arXiv, May 31, 2023. Accessed: Nov. 13, 2023. [Online]. Available: http://arxiv.org/abs/2301.11699