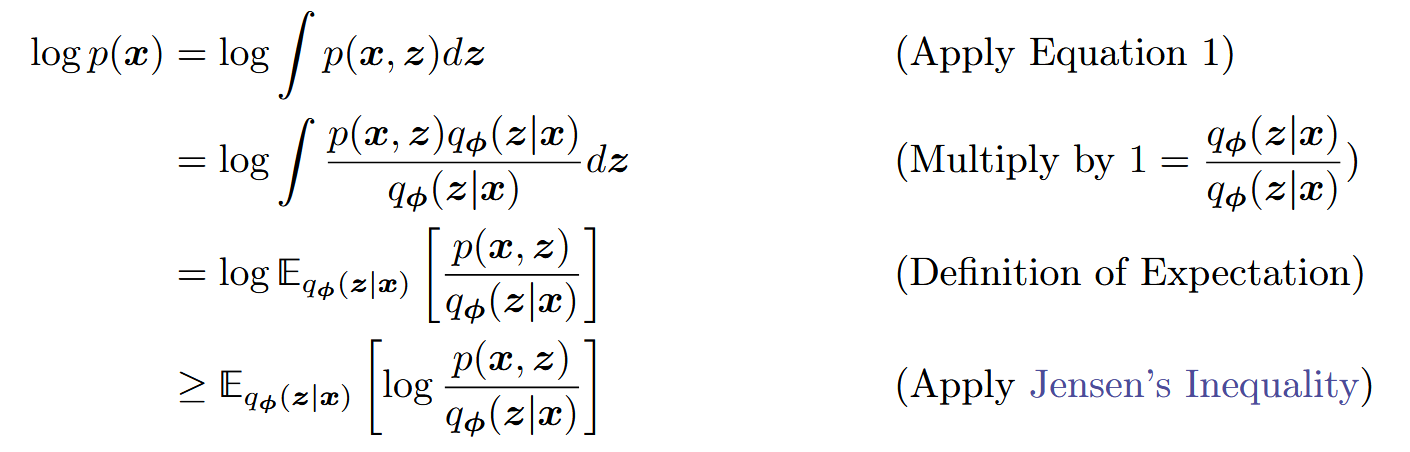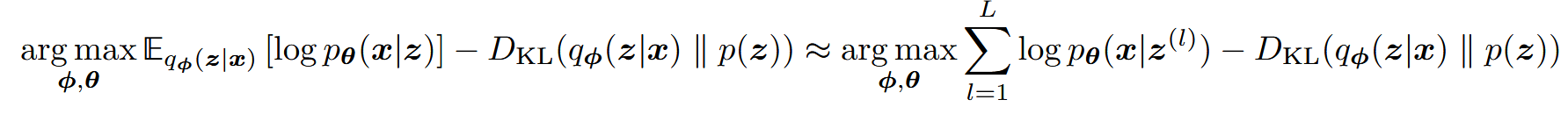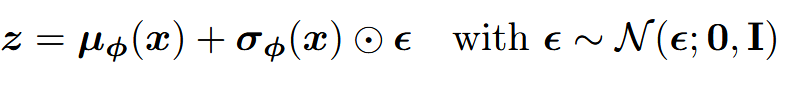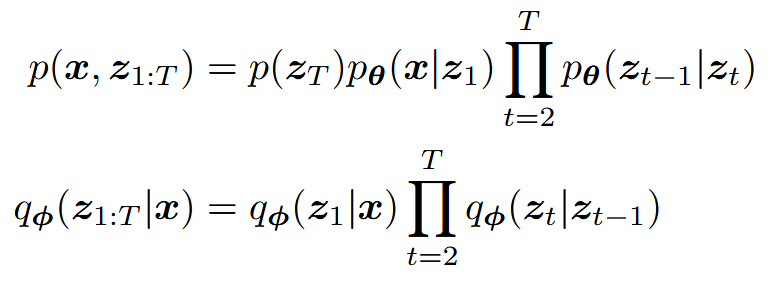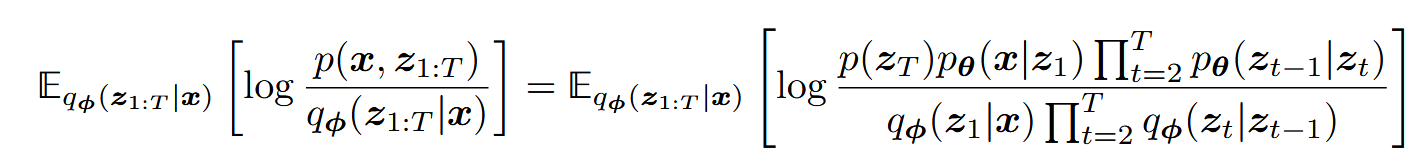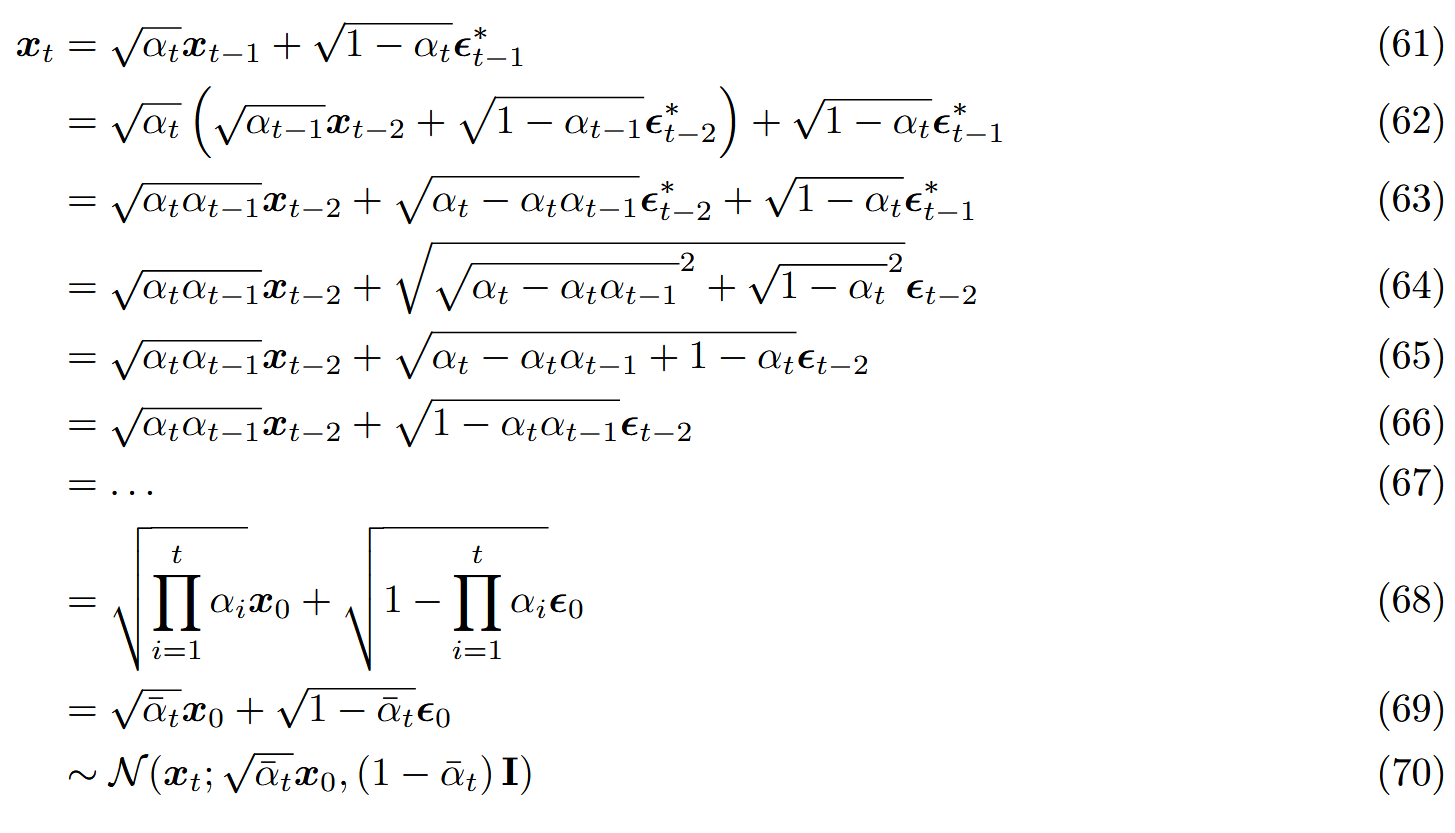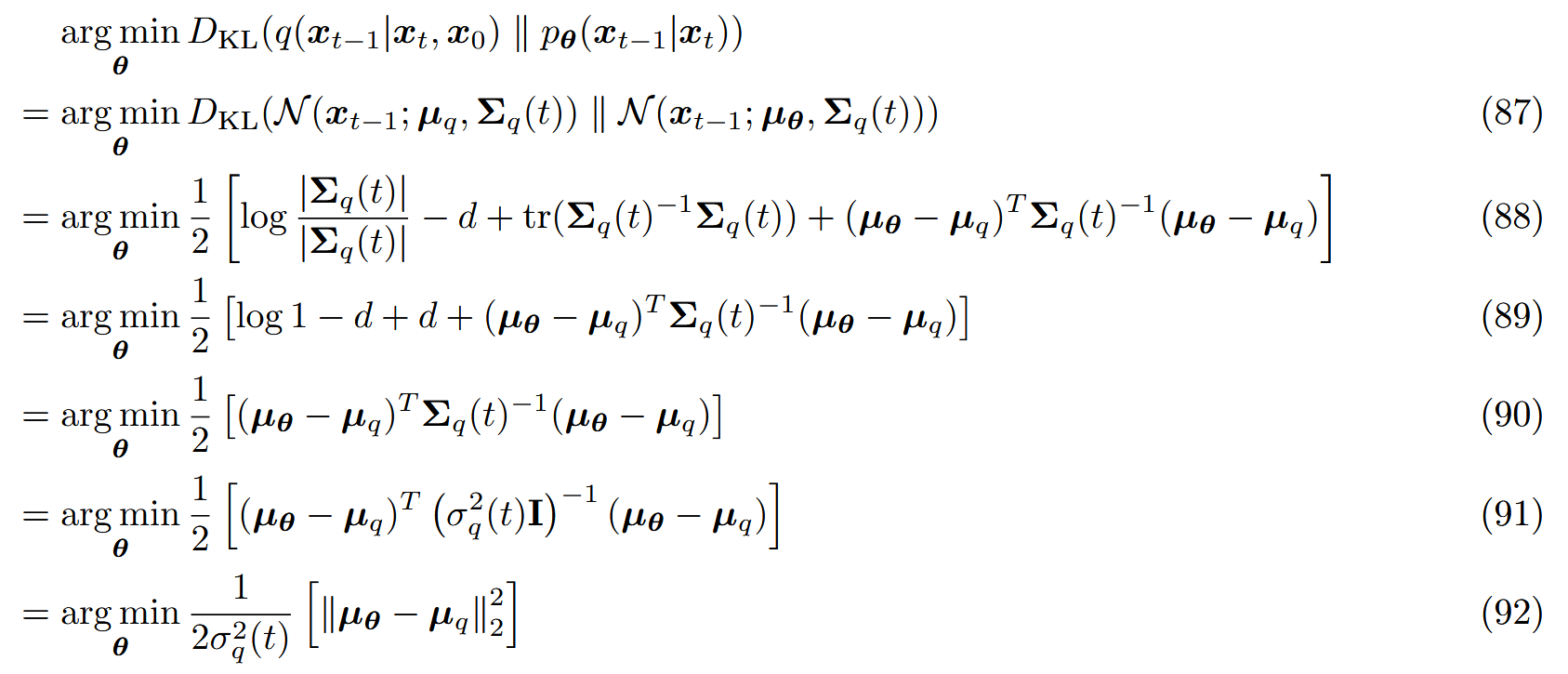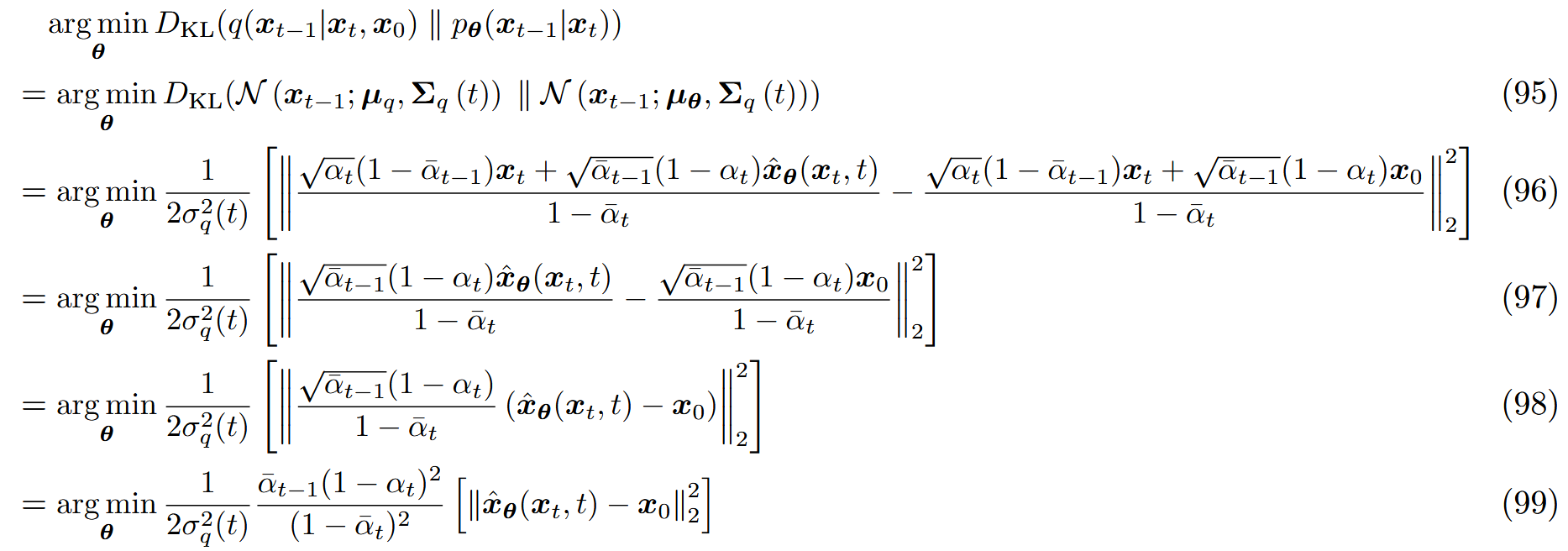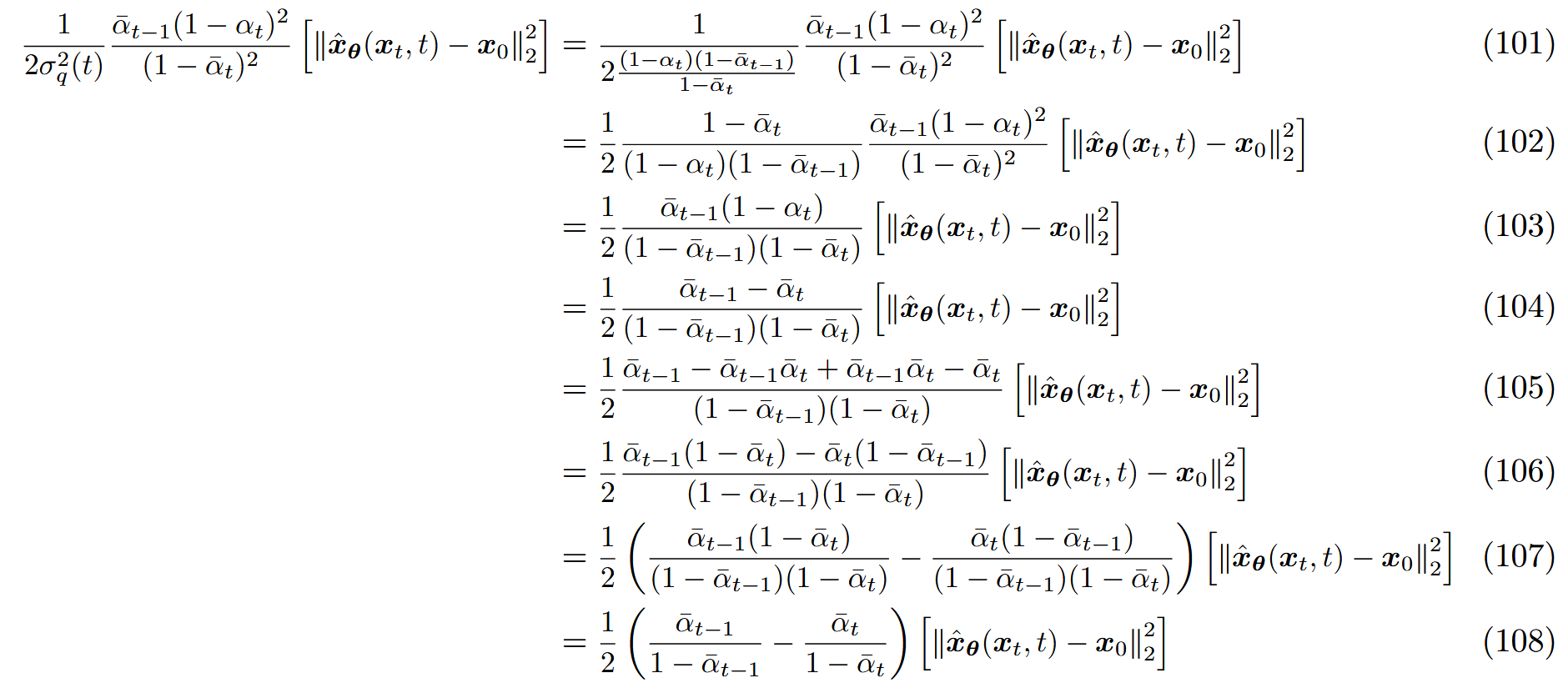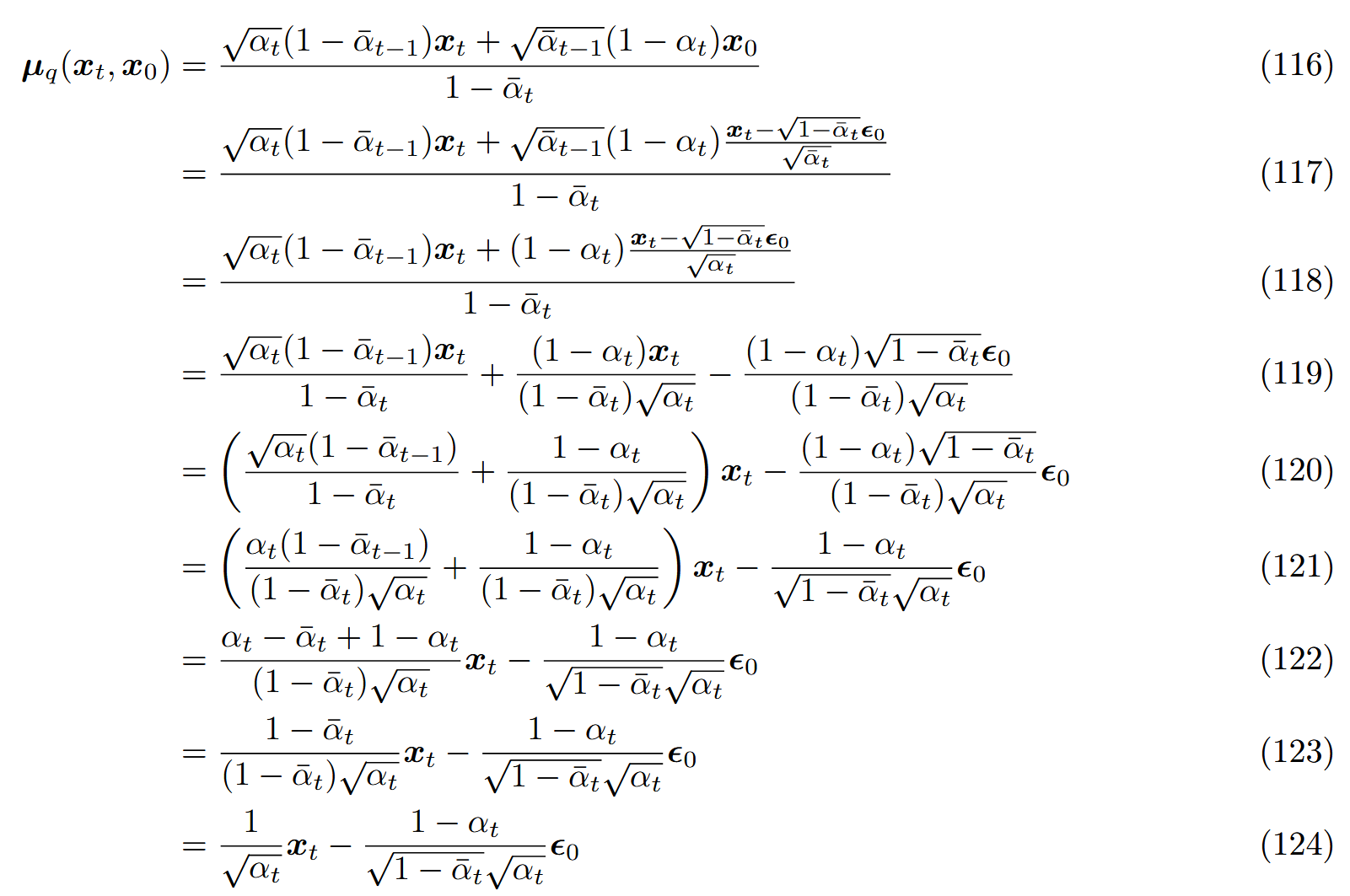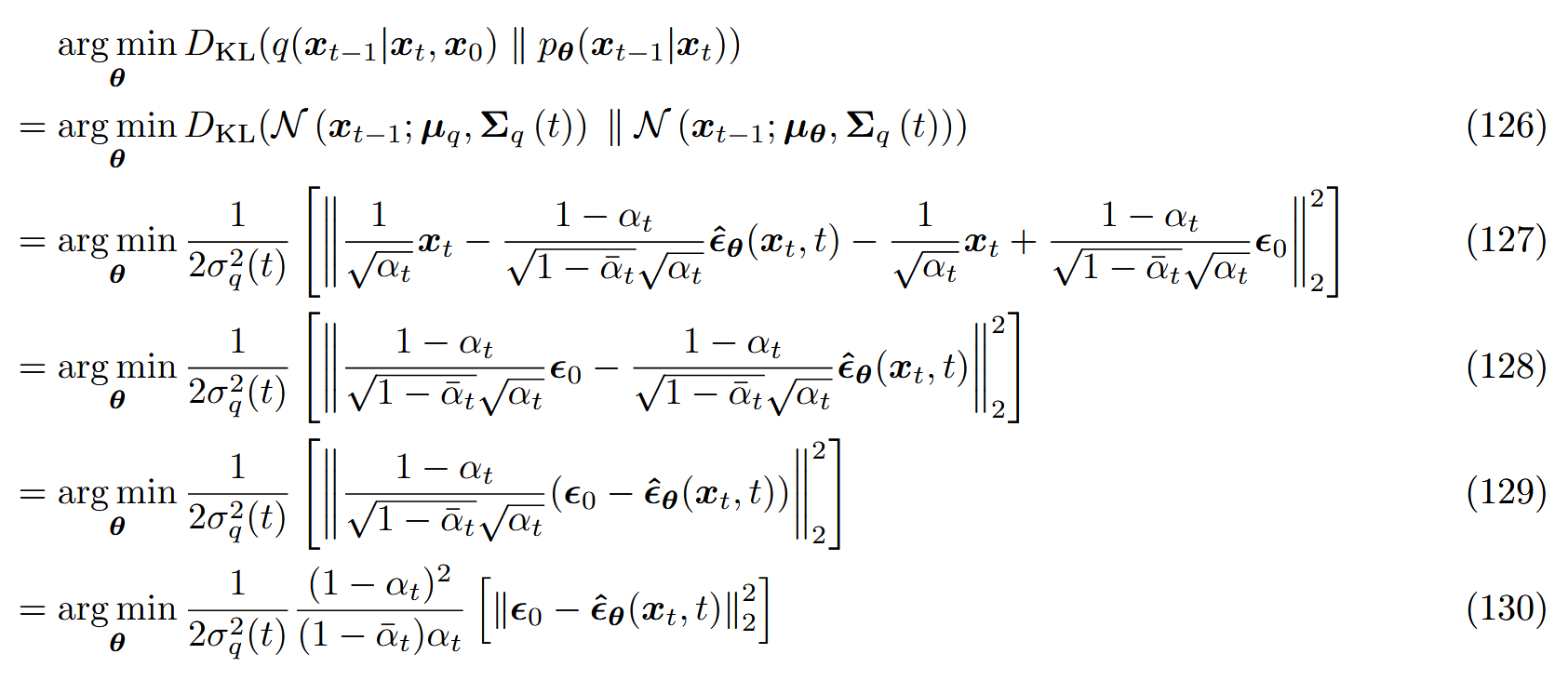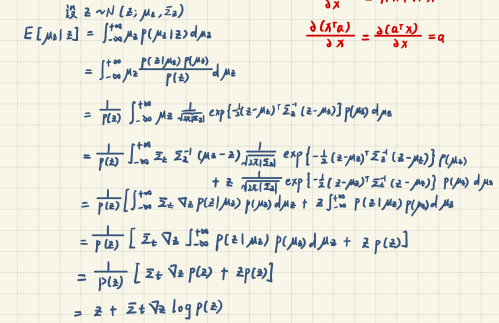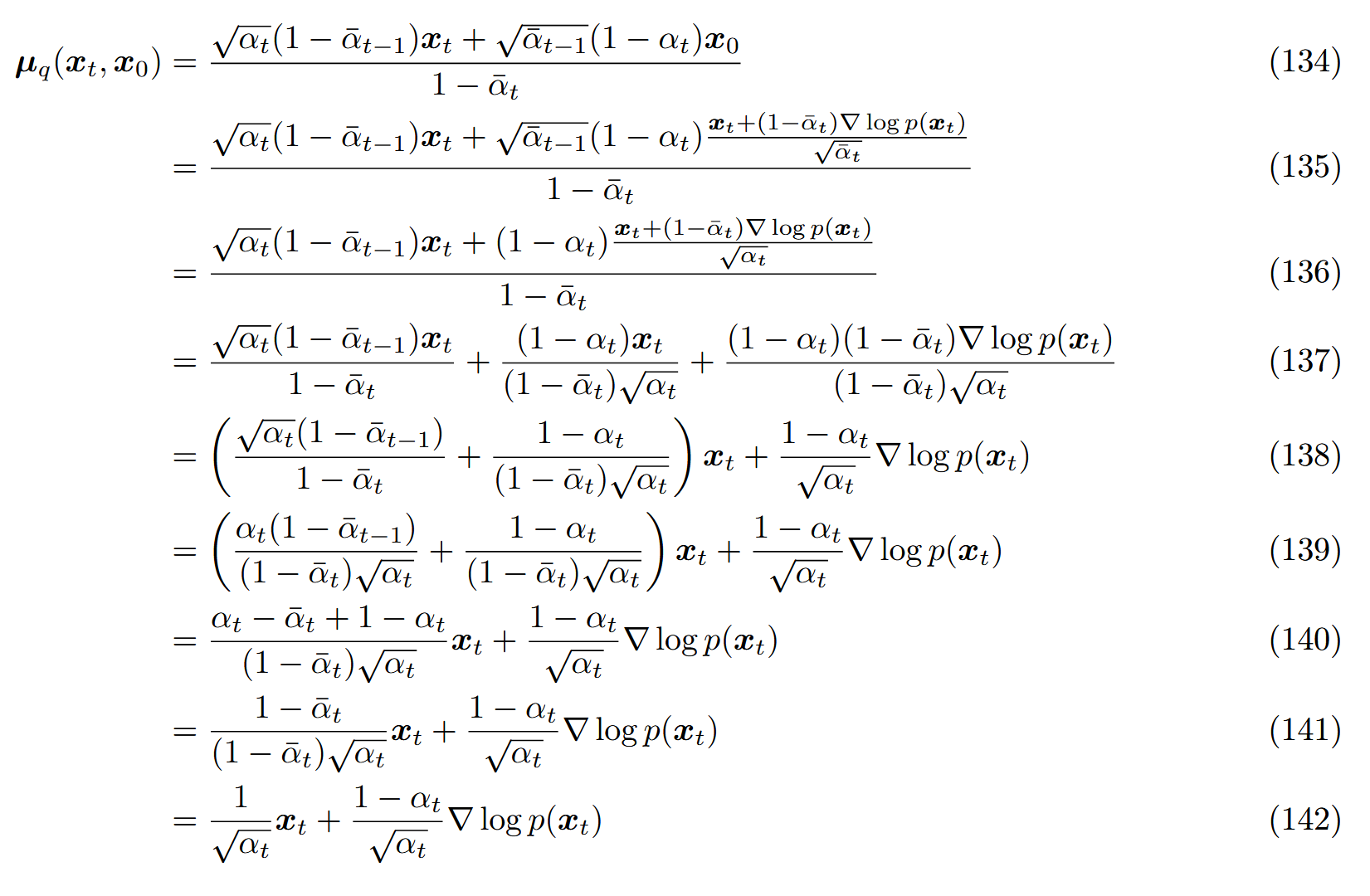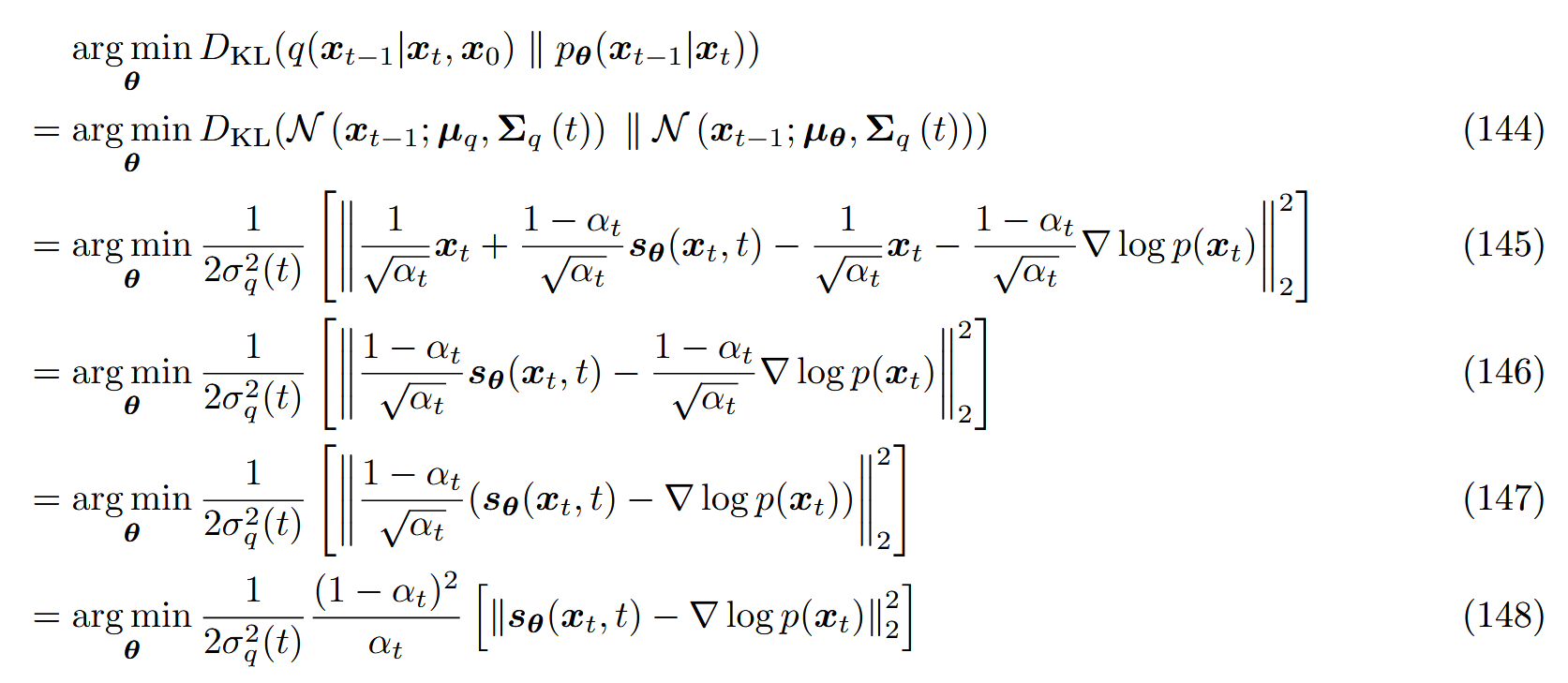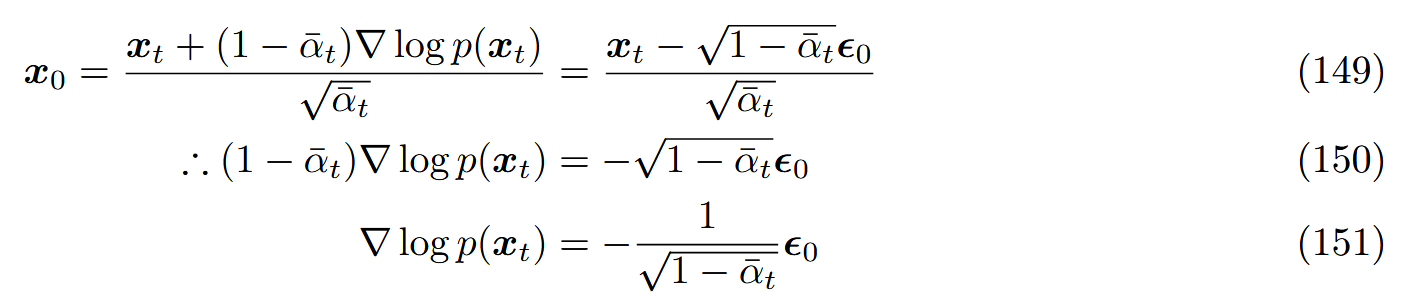Understanding Diffusion Models: A Unified Perspective
ELBO
目标:学习一个模型去最大化 p ( x ) p(x) p ( x )
法一:p ( x ) = ∫ p ( x , z ) d z p(x)=\int p(x,z)dz p ( x ) = ∫ p ( x , z ) d z
法二:p ( x ) = p ( x , z ) p ( z ∣ x ) p(x)=\frac{p(x,z)}{p(z|x)} p ( x ) = p ( z ∣ x ) p ( x , z )
代理目标:最大化ELBO
log p ( x ) ≥ E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] \log{p(x)} \ge \mathbb E_{q_\phi(z|x)}\Big[\log{\frac{p(x,z)}{q_\phi(z|x)}}\Big]
log p ( x ) ≥ E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ]
why?
使用法一证明:
并不能告诉我们太多幕后实际情况的有用信息,而且这个证明并没有直观的给出究竟为什么ELBO实际上是证据的下限
于是使用法二证明:
因此证据就等于ELBO加上KL散度
log p ( x ) \log{p(x)} log p ( x ) ϕ \phi ϕ 最大化ELBO项就相当于最小化KL散度项
VAE
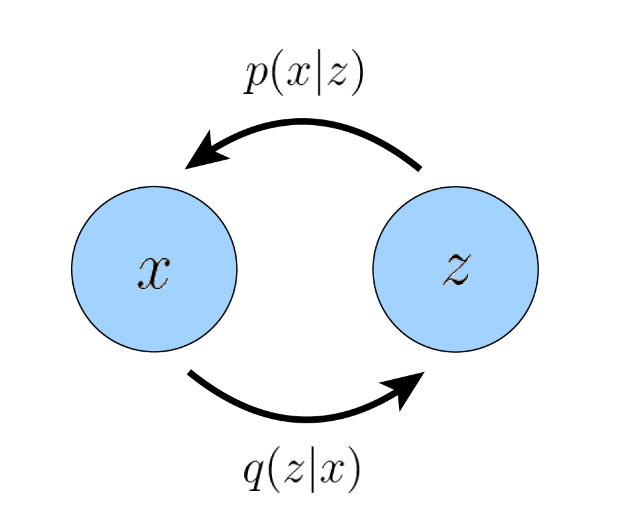
输入数据经过中间的bottleneck表示步骤后被训练来预测它本身
encoder :学习中间的bottleneck分布 q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
decoder : 学习确定的函数 p θ ( x ∣ z ) p_\theta(x|z) p θ ( x ∣ z ) z z z x x x
第一项衡量变分分布的decoder的重建似然,保证学到的分布可以建模有效的可以重新生成原始数据的潜在变量;第二项衡量学习到的变分分布和潜在变量的先验信念有多相似,最小化该项可以避免学到的分布坍塌为Dirac delta函数
那么最大化ELBO等价于最大化第一项、最小化第二项
VAE的encoder通常通过对数协方差建模一个多元高斯,先验器通常被选择为一个标准高斯:
KL散度项在分析上可以被计算,重建项可以使用蒙特卡罗方法近似,于是目标变为:
由于每个 z z z z z z x x x ϵ \epsilon ϵ
训练VAE后,可以直接从隐空间 p ( z ) p(z) p ( z ) z z z x x x
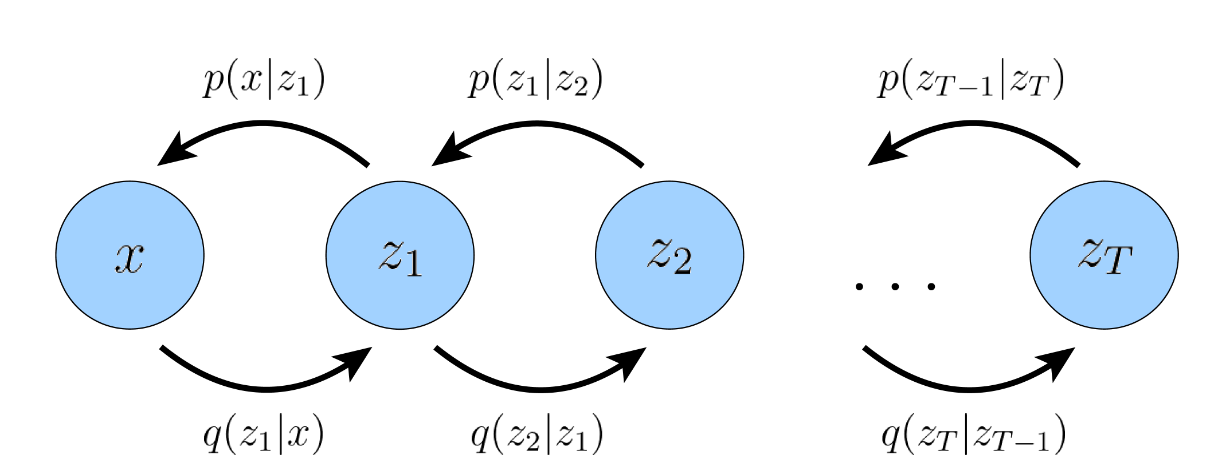
Hierarchical Variational Autoencoders
一般的HVAE有T个层级,每个隐变量都可以以前面的隐变量为条件
decoding每个 z t z_t z t z t + 1 z_{t+1} z t + 1
扩展ELBO为:
代入联合分布、后验器:
变分扩散模型可以更进一步将这个目标分解为可解释的组分
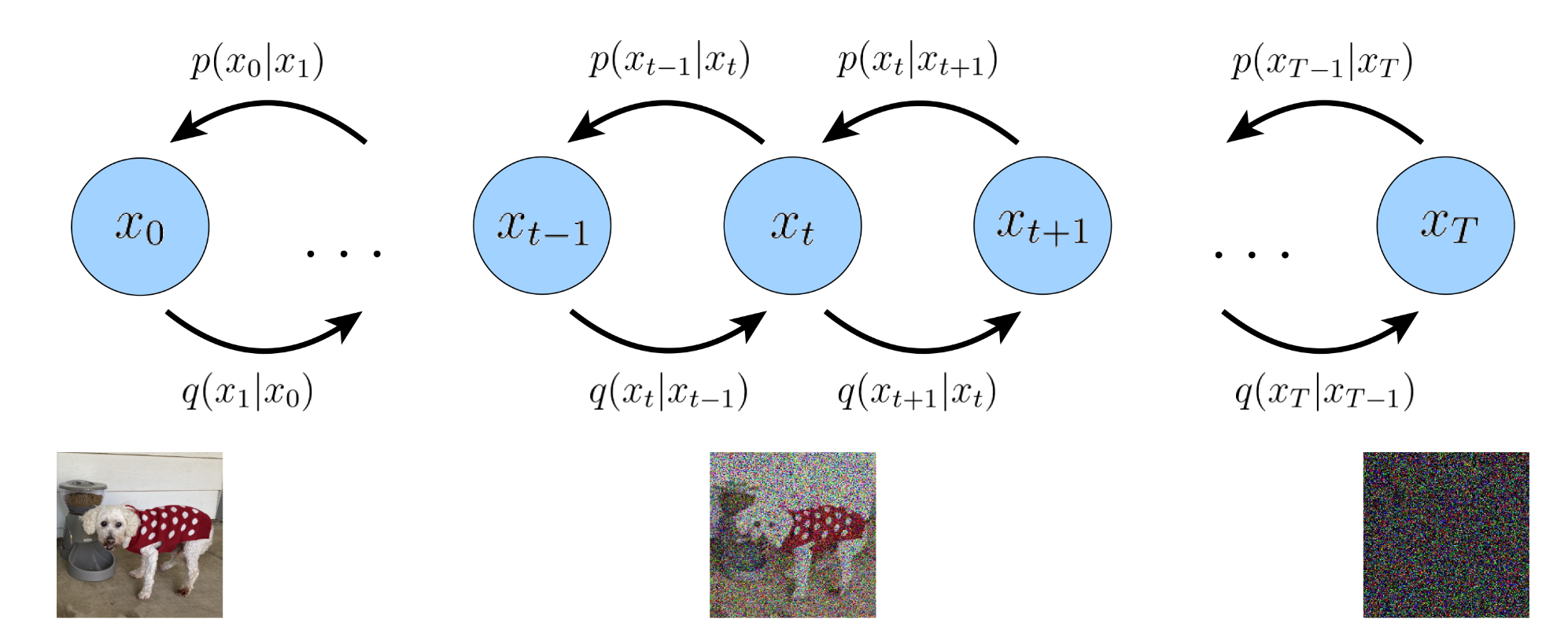
Variational Diffusion Models
三个关键约束:
改写后验器:
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) (30) q(x_{1:T}|x_0)=\prod_{t=1}^{T}q(x_t|x_{t-1})\tag {30}
q ( x 1 : T ∣ x 0 ) = t = 1 ∏ T q ( x t ∣ x t − 1 ) ( 30 )
encoder转移:
q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) (31) q(x_t|x_{t-1})=\mathcal N(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathbf I)\tag{31}
q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) ( 31 )
改写HVAE的联合分布:
p ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) (32) p(x_{0:T})=p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1|x_t})\tag{32}
p ( x 0 : T ) = p ( x T ) t = 1 ∏ T p θ ( x t − 1∣ x t ) ( 32 )
p ( x T ) = N ( x T ; 0 , I ) (33) p(x_T)=\mathcal N(x_T;0,\mathbf I)\tag{33}
p ( x T ) = N ( x T ; 0 , I ) ( 33 )
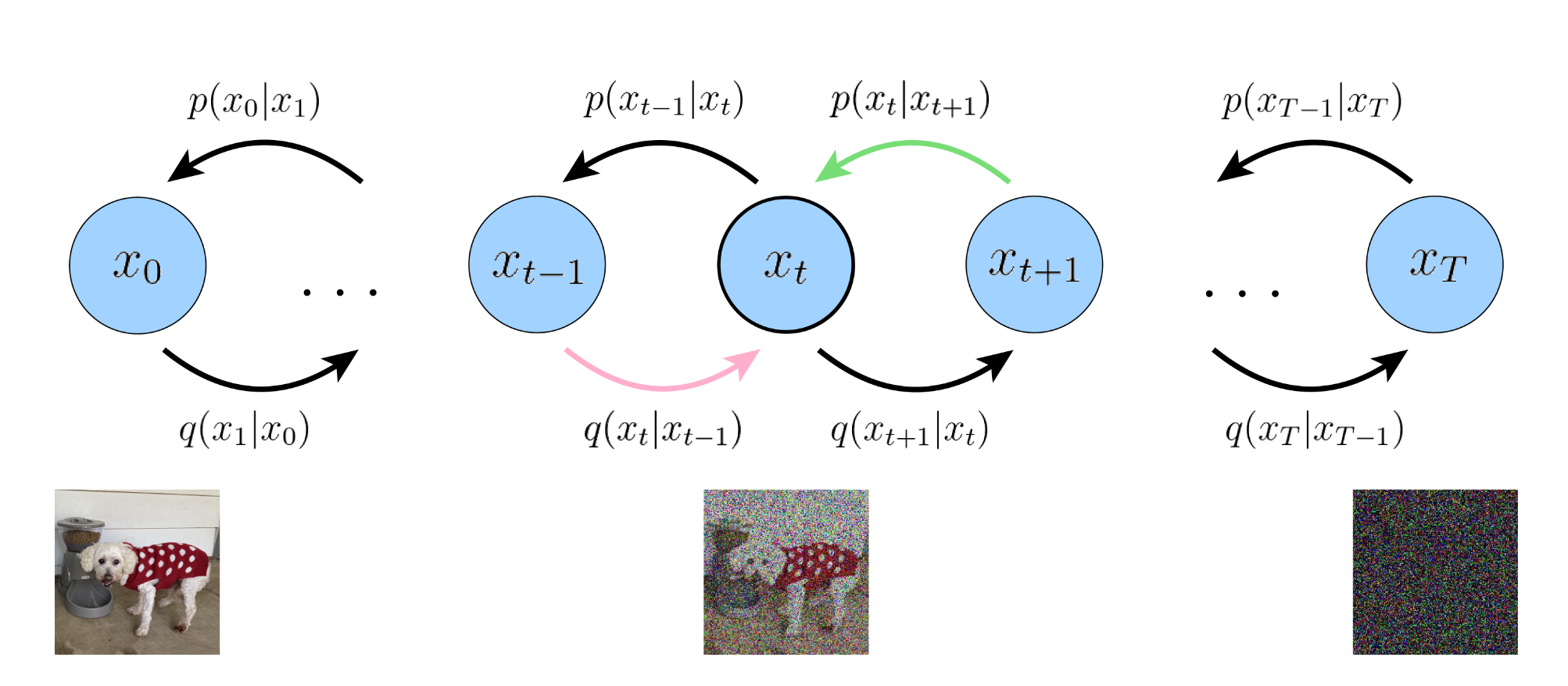
逐渐地添加噪声破坏图像,直至其最终与纯高斯噪声完全相同
VDM的采样过程变为:从p ( x T ) p(x_T) p ( x T ) p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) p θ ( x t − 1 ∣ x t ) x 0 x_0 x 0
重建项 预测给定第一步隐变量后原始数据的对数似然;先验匹配项 不需要被优化,假设一个足够大的T,最后的分布为高斯分布,这项实际上为0;一致项 使得一张噪声图的去噪步应该匹配一张干净图的加噪步:
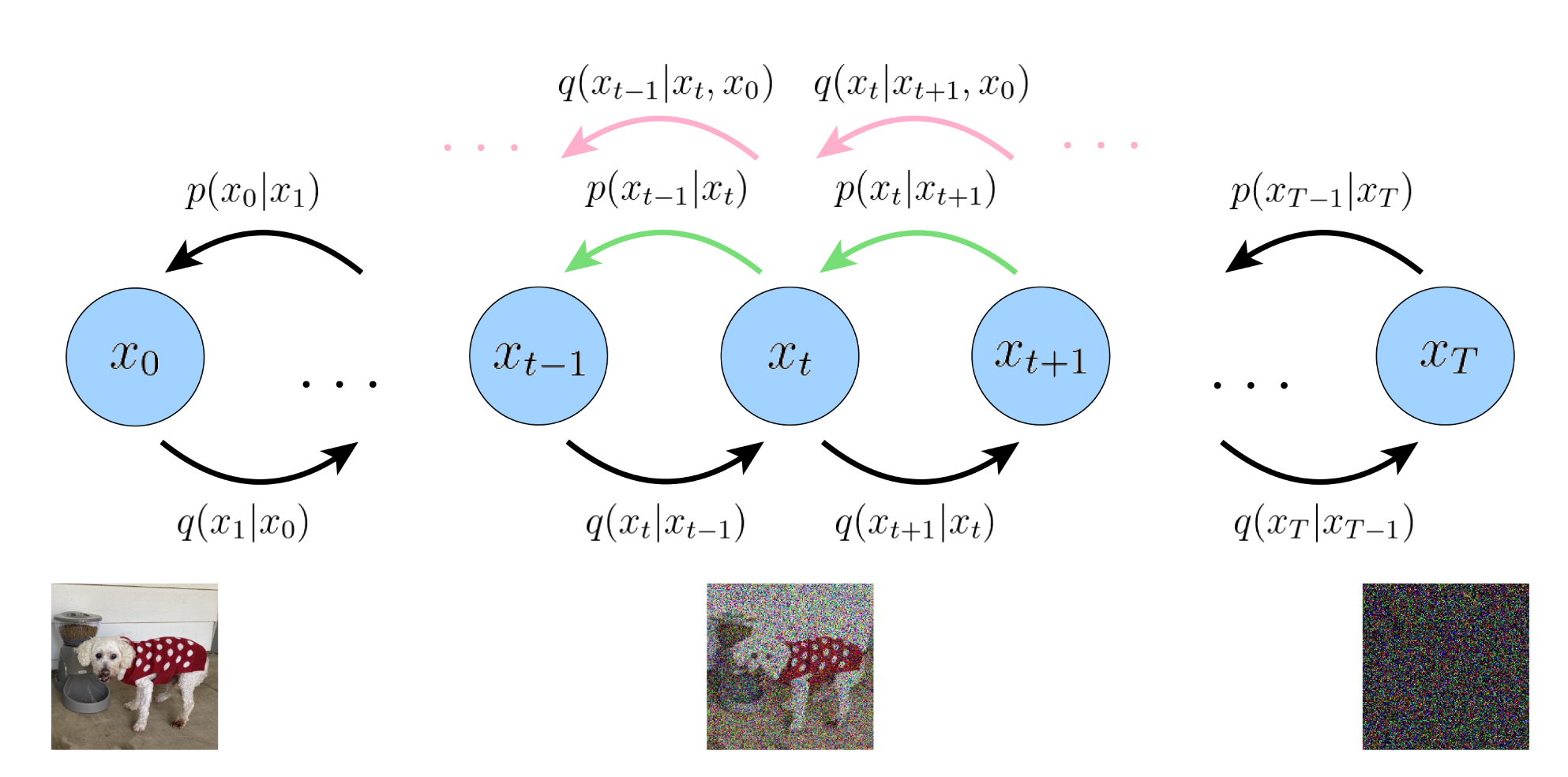
上面的结果是可能是次优解,由于一致项作为一个期望在每个时间步有两个随机变量,使用蒙特卡洛估计可能会有较高的方差。改进方案:将encoder转移改写为 q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) q(x_t|x_{t-1})=q(x_t|x_{t-1},x_0) q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) 根据贝叶斯规则继续改写:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) (46) q(x_t|x_{t-1},x_0)=\frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}\tag{46}
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) ( 46 )
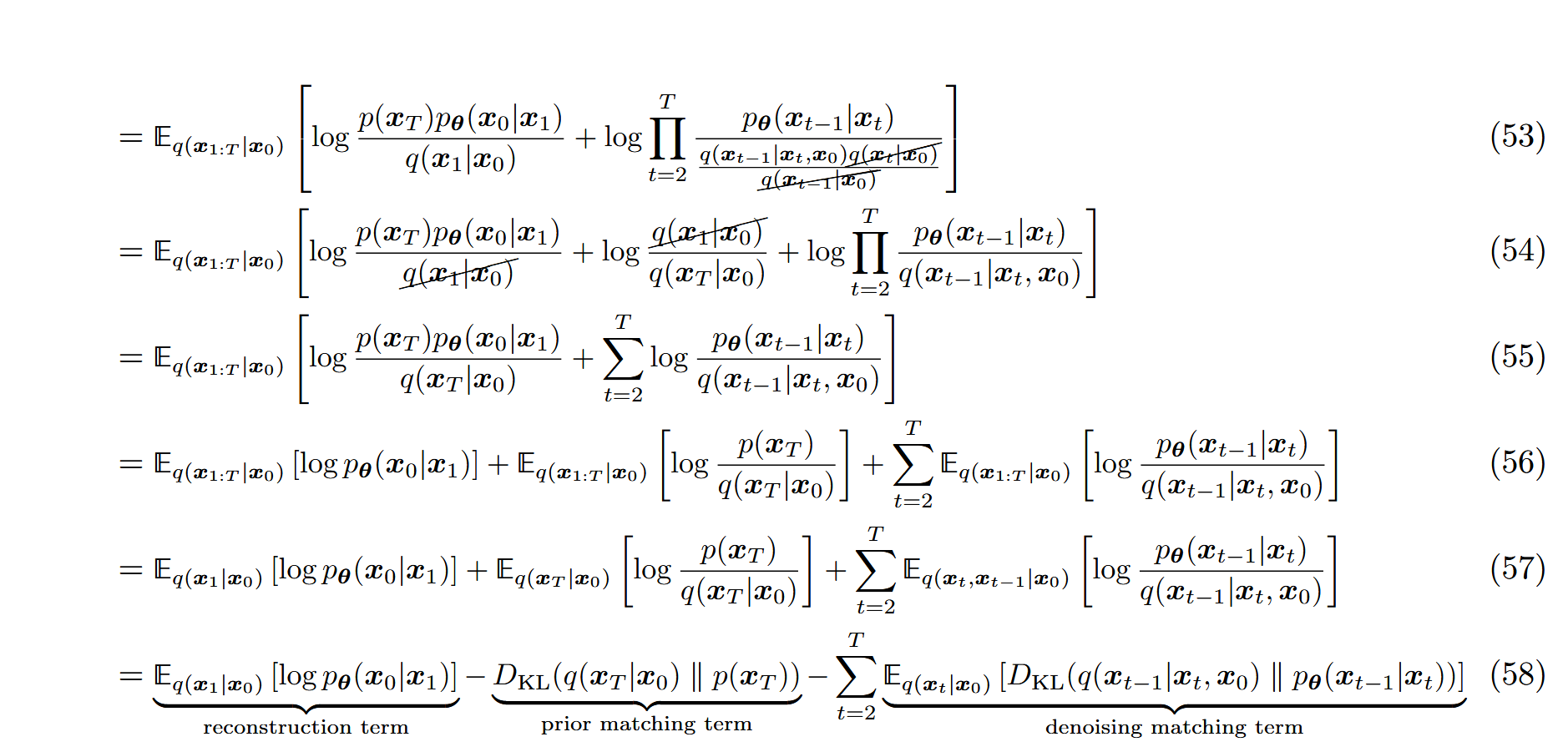
重新进行推导ELBO:
重建项 与普通的VAE相似,可以使用蒙特卡洛估计来近似;先验匹配项 表示最终的噪声分布与标准高斯先验分布有多接近,同样的不需要训练,根据假设同样趋于0;去噪匹配项 中的 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q ( x t − 1 ∣ x t , x 0 ) x t x_t x t x 0 x_0 x 0
去噪匹配项 中的KL散度难以计算,但是可以使用高斯转移的假设进行优化,根据贝叶斯规则:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q(x_{t-1}|x_t,x_0)=\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x 0 ) q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 )
q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) q(x_t|x_{t-1})=q(x_t|x_{t-1})=\mathcal N(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathbf I) q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) x t ∼ q ( x t ∣ x t − 1 ) x_t\sim q(x_t|x_{t-1}) x t ∼ q ( x t ∣ x t − 1 )
x t = α t x t − 1 + 1 − α t ϵ (59) x_t=\sqrt \alpha_tx_{t-1}+\sqrt{1-\alpha_t}\epsilon\tag{59}
x t = α t x t − 1 + 1 − α t ϵ ( 59 )
x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 ϵ (60) x_{t-1}=\sqrt \alpha_{t-1}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon\tag{60}
x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 ϵ ( 60 )
于是:
代入得:
将方差重写,Σ q ( t ) = σ q 2 ( t ) I \Sigma_q(t)=\sigma_q^2(t)\mathbf I Σ q ( t ) = σ q 2 ( t ) I
σ q 2 ( t ) = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t (85) \sigma_q^2(t)=\frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\tag{85}
σ q 2 ( t ) = 1 − α ˉ t ( 1 − α t ) ( 1 − α ˉ t − 1 ) ( 85 )
为了匹配近似ground-truth去噪转移步 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q ( x t − 1 ∣ x t , x 0 ) ,将近似 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_{t}) p θ ( x t − 1 ∣ x t ) 也建模为高斯分布。由于 α \alpha α Σ q ( t ) = σ q 2 ( t ) I \Sigma_q(t)=\sigma_q^2(t)\mathbf I Σ q ( t ) = σ q 2 ( t ) I .因此必须参数化它的均值 μ θ ( x t , t ) \mu_\theta(x_t,t) μ θ ( x t , t ) .
两个高斯分布之间的KL散度:
D K L ( N ( x ; μ x , Σ x ) ∥ N ( y ; μ y , Σ y ) ) = 1 2 [ log ∣ Σ y ∣ ∣ Σ x ∣ − d + t r ( Σ y − 1 Σ x ) + ( μ y − μ x ) T Σ y − 1 ( μ y − μ x ) ] (86) D_{KL}(\mathcal N(x;\mu_x,\Sigma_x)\parallel\mathcal N(y;\mu_y,\Sigma_y))=\frac{1}{2}\bigg[\log\frac{|\Sigma_y|}{|\Sigma_x|}-d+tr(\Sigma_y^{-1}\Sigma_x)+(\mu_y-\mu_x)^T\Sigma_y^{-1}(\mu_y-\mu_x)\bigg]\tag{86}
D K L ( N ( x ; μ x , Σ x ) ∥ N ( y ; μ y , Σ y )) = 2 1 [ log ∣ Σ x ∣ ∣ Σ y ∣ − d + t r ( Σ y − 1 Σ x ) + ( μ y − μ x ) T Σ y − 1 ( μ y − μ x ) ] ( 86 )
那么去噪匹配项 中的KL散度可以通过最小化这两个分布的均值 差异来减小:
μ q ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t (93) \mu_q(x_t,x_0)=\frac{\sqrt\alpha_t(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1-\bar\alpha_t}\tag{93}
μ q ( x t , x 0 ) = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 ( 93 )
μ θ ( x t , t ) = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x ^ θ ( x t , t ) 1 − α ˉ t (94) \mu_\theta(x_t,t)=\frac{\sqrt\alpha_t(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)\hat x_\theta(x_t,t)}{1-\bar\alpha_t}\tag{94}
μ θ ( x t , t ) = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x ^ θ ( x t , t ) ( 94 )
因此优化问题简化为:
因此优化VDM归结起来就是学习一个NN从任意噪声版本的图像中预测出原始图像。此外,最小化所有噪声水平上公式( 58 ) (58) ( 58 )
a r g m i n θ E t ∼ U 2 , T [ E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] ] (100) \underset{\theta}{arg\ min}\ \mathbb E_{t\sim U{2,T}}\big[\mathbb E_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)\parallel p_\theta(x_{t-1}|x_t))]\big]\tag{100}
θ a r g min E t ∼ U 2 , T [ E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ))] ] ( 100 )
可以在每个时间步使用随机采样来优化。
学习噪声参数
如何学习噪声参数?一种方法是使用一个NN α ^ η ( t ) \hat\alpha_\eta(t) α ^ η ( t ) α t \alpha_t α t
由于 q ( x t ∣ x 0 ) ∼ N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t|x_0)\sim \mathcal N(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)\mathbf I) q ( x t ∣ x 0 ) ∼ N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) S N R = μ 2 σ 2 \mathrm{SNR}=\frac{\mu^2}{\sigma^2} SNR = σ 2 μ 2
S N R ( t ) = α ˉ t 1 − α ˉ t (109) \mathrm{SNR}(t)=\frac{\bar\alpha_t}{1-\bar\alpha_t}\tag{109}
SNR ( t ) = 1 − α ˉ t α ˉ t ( 109 )
1 2 σ q 2 ( t ) α ˉ t − 1 ( 1 − α t ) 2 ( 1 − α ˉ t ) 2 [ ∥ x ^ θ ( x t , t ) − x 0 ∥ 2 2 ] = 1 2 ( S N R ( t − 1 ) − S N R ( t ) ) [ ∥ x ^ θ ( x t , t ) − x 0 ∥ 2 2 ] (110) \frac{1}{2\sigma_q^2(t)}\frac{\bar\alpha_{t-1}(1-\alpha_t)^2}{(1-\bar\alpha_t)^2}\Big[\left\|\hat x_\theta(x_t,t)-x_0\right\|_2^2\Big]=\frac{1}{2}(\mathrm {SNR}(t-1)-\mathrm{SNR}(t))\Big[\left\|\hat x_\theta(x_t,t)-x_0\right\|_2^2\Big]\tag{110}
2 σ q 2 ( t ) 1 ( 1 − α ˉ t ) 2 α ˉ t − 1 ( 1 − α t ) 2 [ ∥ x ^ θ ( x t , t ) − x 0 ∥ 2 2 ] = 2 1 ( SNR ( t − 1 ) − SNR ( t )) [ ∥ x ^ θ ( x t , t ) − x 0 ∥ 2 2 ] ( 110 )
SNR表示原始信号与噪声之间的比值,在扩散中我们需要SNR随着t的增加而减小,于是可以表示为:
S N R ( t ) = e x p ( − ω η ( t ) ) (111) \mathrm{SNR}(t)=exp(-\omega_\eta(t))\tag{111}
SNR ( t ) = e x p ( − ω η ( t )) ( 111 )
ω η ( t ) \omega_\eta(t) ω η ( t ) α ˉ t \bar\alpha_t α ˉ t 1 − α ˉ t 1-\bar\alpha_t 1 − α ˉ t
α ˉ t 1 − α ˉ t = exp ( − ω η ( t ) ) (112) \frac{\bar\alpha_t}{1-\bar\alpha_t}=\exp(-\omega_\eta(t))\tag{112}
1 − α ˉ t α ˉ t = exp ( − ω η ( t )) ( 112 )
∴ α ˉ t = s i g m o i d ( − ω η ( t ) ) (113) \therefore \bar\alpha_t=sigmoid(-\omega_\eta(t))\tag{113}
∴ α ˉ t = s i g m o i d ( − ω η ( t )) ( 113 )
∴ 1 − α ˉ t = s i g m o i d ( ω η ( t ) ) (114) \therefore 1-\bar\alpha_t=sigmoid(\omega_\eta(t))\tag{114}
∴ 1 − α ˉ t = s i g m o i d ( ω η ( t )) ( 114 )
三种等价形式
预测噪声
根据公式 ( 69 ) (69) ( 69 )
x 0 = x t − 1 − α ˉ t ϵ 0 α ˉ t (115) x_0=\frac{x_t-\sqrt{1-\bar\alpha_t}\epsilon_0}{\sqrt{\bar\alpha_t}}\tag{115}
x 0 = α ˉ t x t − 1 − α ˉ t ϵ 0 ( 115 )
代入到均值 μ q ( x t , x 0 ) \mu_q(x_t,x_0) μ q ( x t , x 0 ) :
于是近似的均值 μ θ ( x t , t ) \mu_\theta(x_t,t) μ θ ( x t , t ) :
μ θ ( x t , t ) = 1 α t x t − 1 − α t 1 − α ˉ t α t ϵ ^ θ ( x t , t ) (125) \mu_\theta(x_t,t)=\frac{1}{\sqrt\alpha_t}x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}\sqrt\alpha_t}\hat\epsilon_\theta(x_t,t)\tag{125}
μ θ ( x t , t ) = α t 1 x t − 1 − α ˉ t α t 1 − α t ϵ ^ θ ( x t , t ) ( 125 )
那么优化项就变为:
因此,通过预测原始图像 x 0 x_0 x 0
预测分数
Tweedie公式 给定从指数族分布中的样本的真实平均值可以通过样本的最大似然估计(经验平均值)加上一些涉及估计分数的校正项得到
E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z ) \mathbb E[\mu_z|z]=z+\Sigma_z\nabla_z\log p(z)
E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z )
在VDM里面,通常被用来减少样本的偏差,如果观测样本都在潜在分布的一端,那么负的分数将会变大并且校正原始的样本的最大似然估计为正确的均值。我们使用它来预测给定后验器样本后的 x t x_t x t q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t|x_0)=\mathcal N(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)\mathbf I) q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I )
E [ μ x t ∣ x t ] = x t + ( 1 − α ˉ t ) ∇ x t log p ( x t ) (131) \mathbb E[\mu_{x_t}|x_t]=x_t+(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t)\tag{131}
E [ μ x t ∣ x t ] = x t + ( 1 − α ˉ t ) ∇ x t log p ( x t ) ( 131 )
于是:
α ˉ t x 0 = x t + ( 1 − α ˉ t ) ∇ log p ( x t ) (132) \sqrt{\bar\alpha_t}x_0=x_t+(1-\bar\alpha_t)\nabla\log p(x_t)\tag{132}
α ˉ t x 0 = x t + ( 1 − α ˉ t ) ∇ log p ( x t ) ( 132 )
∴ x 0 = x t + ( 1 − α ˉ t ) ∇ log p ( x t ) α ˉ t (133) \therefore x_0=\frac{x_t+(1-\bar\alpha_t)\nabla\log p(x_t)}{\sqrt{\bar\alpha_t}}\tag{133}
∴ x 0 = α ˉ t x t + ( 1 − α ˉ t ) ∇ log p ( x t ) ( 133 )
再次代入到均值 μ q ( x t , x 0 ) \mu_q(x_t,x_0) μ q ( x t , x 0 ) :
于是近似的均值 μ θ ( x t , t ) \mu_\theta(x_t,t) μ θ ( x t , t ) :
μ θ ( x t , t ) = 1 α t x t + 1 − α t α t s θ ( x t , t ) (143) \mu_\theta(x_t,t)=\frac{1}{\sqrt\alpha_t}x_t+\frac{1-\alpha_t}{\sqrt\alpha_t}s_\theta(x_t,t)\tag{143}
μ θ ( x t , t ) = α t 1 x t + α t 1 − α t s θ ( x t , t ) ( 143 )
那么优化项就变为:
在这里,s θ ( x t , t ) s_\theta(x_t,t) s θ ( x t , t ) ∇ x t log p ( x t ) \nabla_{x_t}\log p(x_t) ∇ x t log p ( x t ) t t t x t x_t x t
二者联系
可以看到,两者之间存在一个随时间变化的常数因子!分数函数衡量应该在数据空间中如何移动来最大化对数似然;
“intuitively, since the source noise is added to a natural image to corrupt it, moving in its opposite direction “denoises” the image and would be the best update to increase the subsequent log probability.” (Luo, 2022, p. 17 🔤直观上,由于源噪声被添加到自然图像中以破坏它,因此沿其相反方向移动会对图像进行“去噪”,并且将是增加后续对数概率的最佳更新。🔤
于是,学习建模分数函数就等价于建模原噪声的负值(乘上一个比例因子)
因此,我们有三种等价目标:预测原始图像 x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0 ∇ log p ( x 0 ) \nabla\log p(x_0) ∇ log p ( x 0 )
参考
[1] Z. Luo, F. K. Gustafsson, Z. Zhao, J. Sjölund, and T. B. Schön, “Image Restoration with Mean-Reverting Stochastic Differential Equations.” arXiv, May 31, 2023. Accessed: Nov. 13, 2023. [Online]. Available: http://arxiv.org/abs/2301.11699