CCSR

Improving the Stability of Diffusion Models for Content Consistent Super-Resolution

背景

• 过去方法的主要假设是简单已知的退化（双线性下采样、高斯模糊下采样），因此主要集中于改进网络骨干设计。（SRCNN，DnCNN）

• 真实世界应用中总是会有复杂未知的退化。

• 像素级的损失：L1 loss 与 MSE loss 会使得生成结果过于平滑；SSIM loss 以及感知损失可以缓解；对抗损失使得SR结果的细节更加丰富真实，但是面对自然图像往往会有一些伪影，因为自然图像的先验空间比特定类的空间更大。

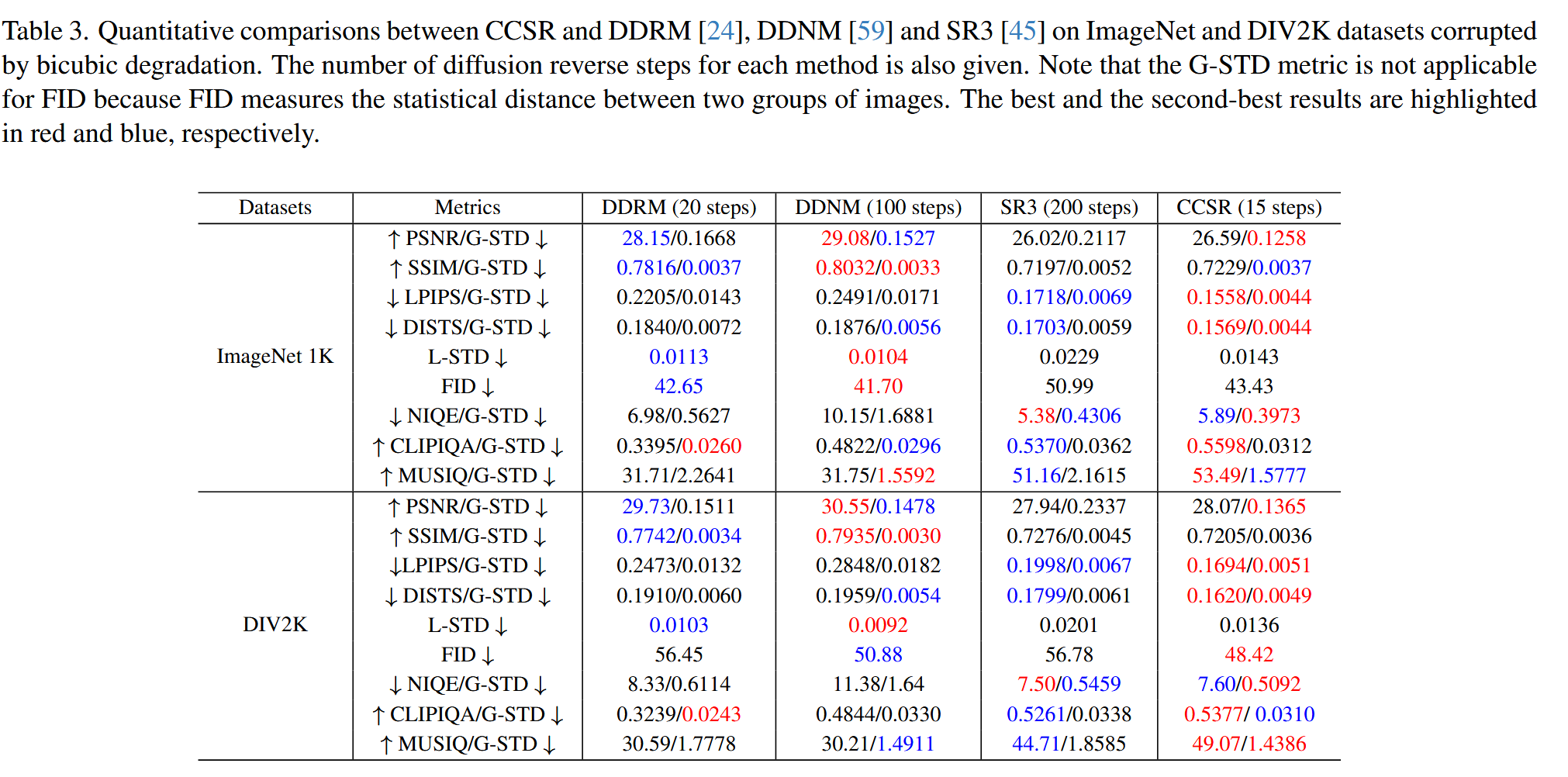
• 扩散模型SR3, DDRM, DDNM只能处理线性或非线性的退化。

• 使用文生图扩散模型作为先验器通过LR图像作为条件来生成HR图像的方法DiffBIR, Pixel-aware Stable Diffusion, StableSR在生成稳定性与内容一致性方面存在局限性

  

贡献

• 当 LR 图像受到明显的信息损失以及退化时，Diffusion priors 可以生成更加真实合理的内容，而 GAN 可以在此基础上以较小的随机性改进细节。
• 利用 diffusion priors 生成结构，使用对抗训练来改进细节以及纹理
• 在扩散阶段提出 non-uniform timestep 采样策略，提高信息提取的效率以及改进图像结构生成的稳定性。在对抗训练阶段微调一个预训练的 VAE decoder 同时进行解码以及细节增强，不需要额外的训练负担。
• 可以生成更稳定、内容一致的 SR 结果，而且只需要15步采样。

方法

动机，框架

随着反向过程的进行，StableSR的PSNR分数提高——结构改善，随后下降——结构上产生较大的变化；LPIPS分数则一直在提高接近于SwinIR-GAN。SwinIR-l1的PSNR分数最高，但是效果最差。当结构信息足够多时，SwinIR-GAN的结果与StableSR的表现相近，都可以忠实地还原图像内容。

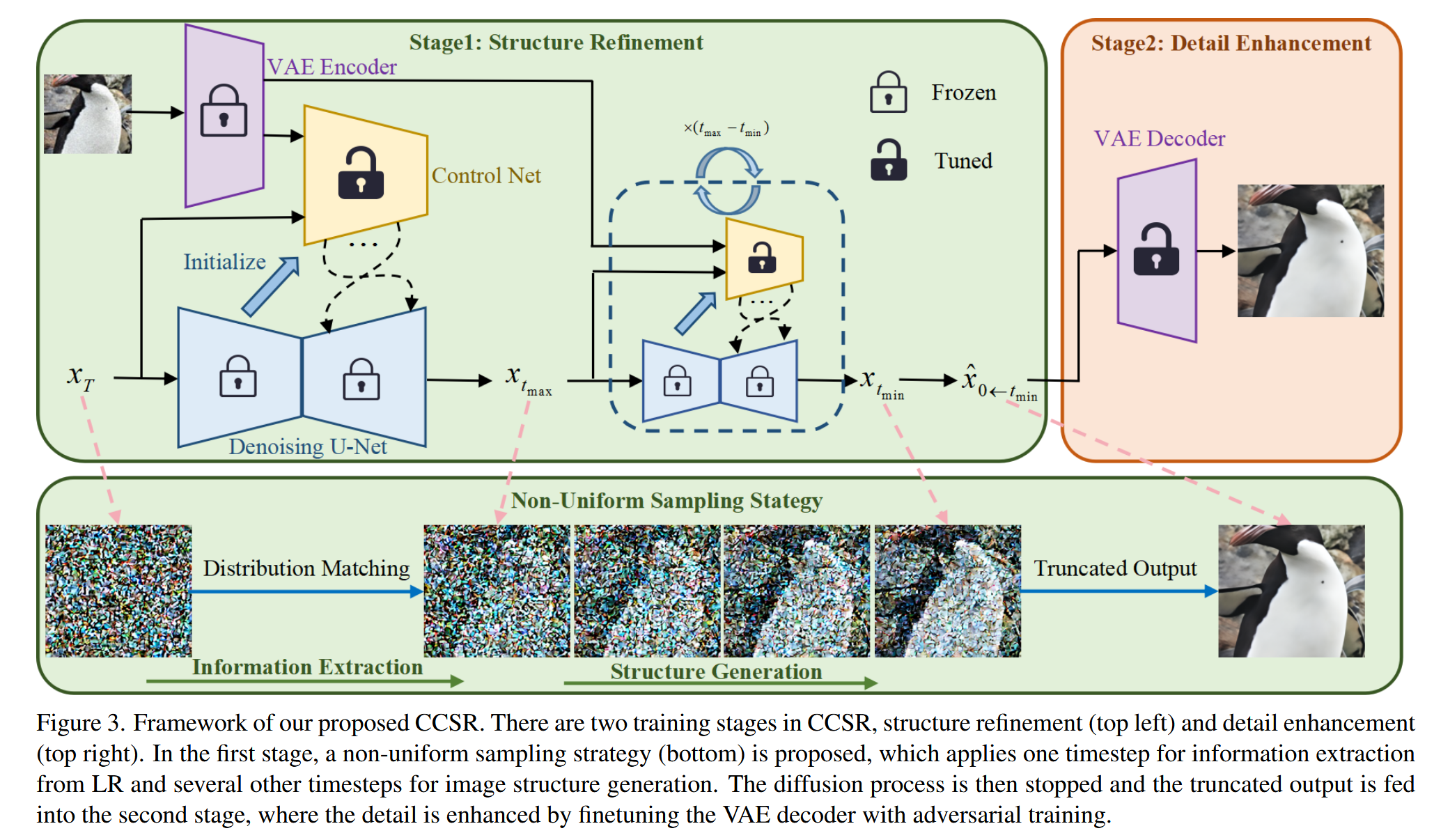
基于以上的观察，本文提出content-consistent super-resolution (CCSR)，第一阶段使用扩散模型来细化图像结构，第二阶段使用对抗训练改进细节。在第一阶段中提出 non-uniform sampling strategy，使用一步来提取LR图像中的细节，剩下的时间步中去进行结构生成，喂入第二阶段生成真实的细节，使用对抗损失微调一个VAE decoder。

Structure Refinement Stage

扩散训练时的损失：

$$l_{diff}=\left\|\epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t}\cdot x_0+\sqrt{1-\bar\alpha_t\cdot\epsilon})\right\|_2^2\tag{1}$$

大多数使用Text2Image生成方法的SR方法都使用统一的采样策略，然而它们都需要从头到尾地生成每一个像素，在SR任务中LR图像可以提供一个粗略的结构，作者认为当前的采样策略没有充分利用LR的信息，会造成资源的浪费。因此提出non-uniform sampling strategy优化采样过程，首先通过将 $x_T$ 映射为中间带噪声的 $x_{t_{max}}$ ，只需要一步就可以从LR图像中提取出粗略的信息；然后经过几个均匀采样步 $x_{t_{max}}\to x_{t_{min}}$ 后截断扩散过程完成结构生成。最终的第二阶段的输出记为 $\hat x_{0\gets t_{min}}$ 。

Why 截断？

作者认为在中间时刻，图像的结构信息已经被较好地重建了（StableSR-600）。

原来的采样过程：$(T,t_{max})\cup[t_{max},t_{min}]\cup(t_{min},0]$

现在的采样过程：$[t_{max},t_{min}]$

由于从 $T\to t_{max}$ 的步长要很大，因此原高斯假设不成立，直接使用非均匀采样策略的效果会显著下降，因此作者提出约束 $\hat x_{0\gets T}=\frac1{\sqrt{\bar\alpha_T}}(x_T-\sqrt{1-\bar\alpha_T}\cdot\hat\epsilon_T)$ , $\hat\epsilon_T=\epsilon_\theta(x_T,T)$ :

$$l_T=\left\|x_0-\hat x_{0\gets T}\right\|_2^2\tag{2}$$

为了保留扩散的连续性，同时约束 $\hat x_{ t_{max}}=\sqrt{\bar\alpha_{t_{max}}}\cdot\hat x_{0\gets T}+\sqrt{1-\bar\alpha_{t_{max}}}\cdot \epsilon$ :

$$l_{t_{max}}=\left\|x_0-\frac1{\sqrt{\bar\alpha_{t_{max}}}}(\hat x_{t_{max}}-\sqrt{1-\bar\alpha_{t_{max}}}\hat\epsilon_{t_{max}})\right\|^2_2\tag{3}$$

最后，CCSR 在 $t=T$ 时刻的训练损失为：

$$l^T_{diff}=l_{diff}+l_T+l_{t_{max}}\tag{4}$$

其他采样时刻的损失不变。

Detail Enhancement Stage

微调一个已有的VAE decoder，通过对抗训练增强细节。二阶段训练时会冻结一阶段的参数。

$t_{max},t_{min}$ 的设置：

$\frac{2T}{3}\to\frac{T}{3}$

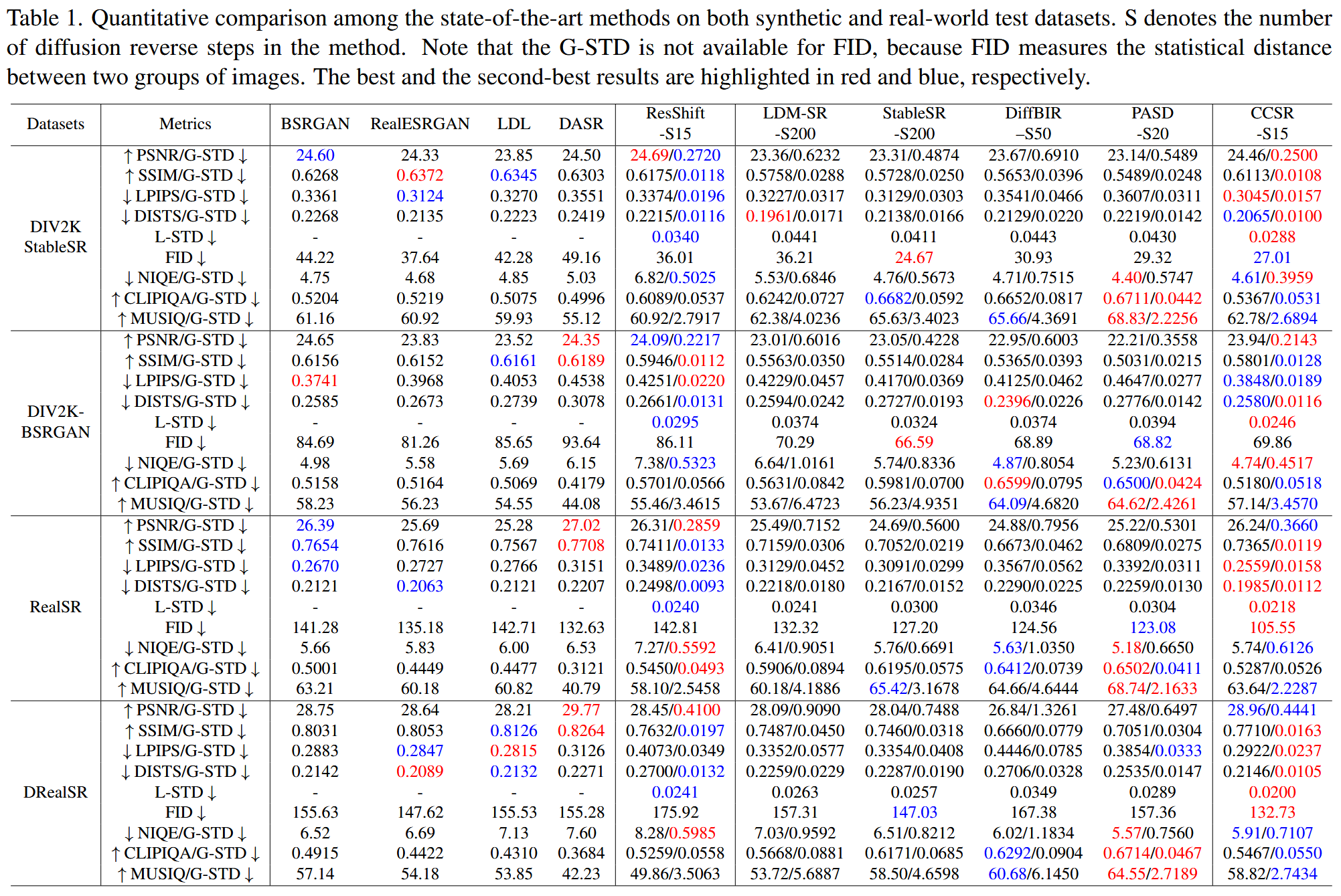
实验

实验设置

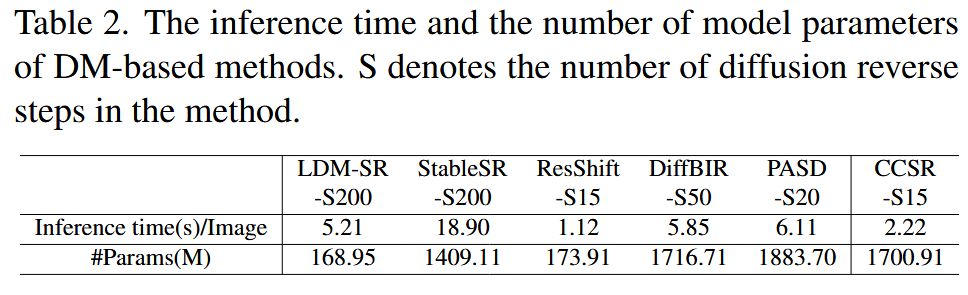
使用基于 Stable Diffusion (SD) 2.1 的 LAControlNet；T=45，因此 CCSR 只需要15步

新的评价标准

global standard deviation (G-STD) 反应图像水平的稳定性

对于每个SR图像，计算它的质量指标以后，对N次运行结果计算 STD ，对所有图像进行平均：

$$\mathrm{G-STD}^p=\frac1M\sum_{j=1}^M\sqrt{\frac{\sum_{j=1}^N(p_i^j-\bar p^j)^2}{N}}\tag{5}$$

local standard deviation (L-STD) 反映局部像素水平的稳定性

对于每个 SR 图像，计算同一位置像素的 STD：

$$\mathrm{L-STD}=\frac{1}{MHW}\sum_{j=1}^M\sum_{h=1}^H\sum_{w=1}^W\sqrt{\frac{\sum_{i=1}^N(x_{i,(h,w)}^j-\bar x_{(h,w)^j}}{N}}\tag{6}$$

参考文献

[1] L. Sun, R. Wu, Z. Zhang, H. Yong, and L. Zhang, “Improving the Stability of Diffusion Models for Content Consistent Super-Resolution.” arXiv, Dec. 30, 2023. Accessed: Jan. 15, 2024. [Online]. Available: http://arxiv.org/abs/2401.00877