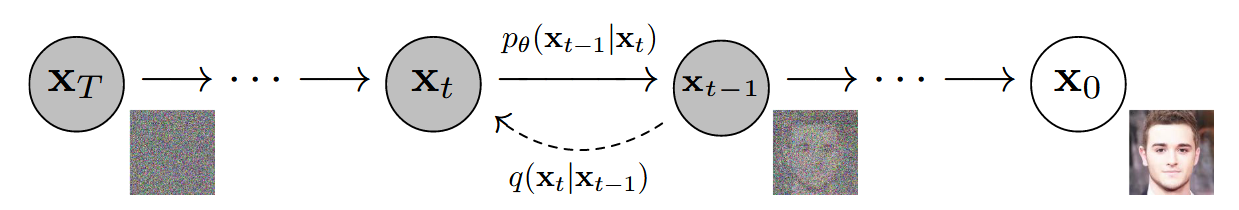扩散模型总结(附代码)
最近在回顾之前写的Understanding Diffusion Models时,发现有个问题,文章太细了,每一步都是数学推导,于是,这篇对其进行一次总结,使得对模型理解一目了然。
前向过程
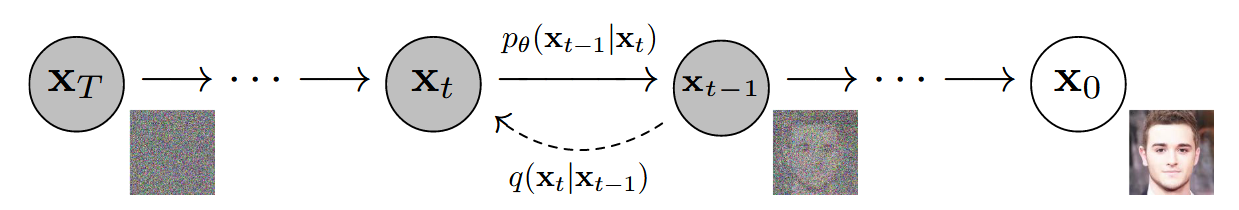
q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I)
x0∼q(x0),β1,...,βT is the variance schedule, αt=1−βt
q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)
αˉt=∏s=1tαs .
xt∼q(xt∣x0) 代码实现:
1
2
3
4
5
6
7
8
9
| def q_xt_x0(self, x0: torch.Tensor, t:torch.tensor):
mean = gather(self.alpha_bar, t) ** 0.5 * x0
var = 1 - gather(self.alpha_bar, t)
return mean, var
def q_sample(self, x0: torch.Tensor, t:torch.tensor, eps: Optional[torch.Tensor] = None):
if eps is None:
eps = torch.randn_like(x0)
mean, var = self.q_xt_x0(x0, t)
return mean + (var ** 0.5) * eps
|
反向过程
q(xt−1∣xt,x0)=N(xt−1;μq(xt,x0),Σq(t))
μq(xt,x0)=αt1xt−1−αˉtαt1−αtϵ0.
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))
μθ(xt,t)=αt1xt−1−αˉtαt1−αtϵ^θ(xt,t), Σq(t)=Σθ(t)=σt2I.
损失
Lsimple(θ)=Et,x0,ϵ[∥ϵ−ϵ^θ(xt,t)∥2]=Et,x0,ϵ[ϵ−ϵ^θ(αˉtx0+1−αˉtϵ,t)2]
代码实现:
1
2
3
4
5
6
7
8
| def loss(self, x0: torch.Tensor, noise: Optional[torch.Tensor] = None):
batch_size = x0.shape[0]
t = torch.randint(0, self.n_steps, (batch_size,), device=x0.device, dtype=torch.long)
if noise is None:
noise = torch.randn_like(x_0)
xt = q_sample(x0, t, eps=noise)
eps_theta = self.eps_model(xt, t)
return F.mse_loss(noise, eps_theta)
|

采样

xt−1∼pθ(xt−1∣xt) 代码实现:
1
2
3
4
5
6
7
8
9
| def p_sample(self,xt: torch.Tensor, t:torch.tensor):
eps_theta = self.eps_model(xt, t)
alpha_bar = gather(self.alpha_bar, t)
alpha = gather(self.alpha, t)
eps_coef = (1 - alpha) / (1 - alpha_bar) ** .5
mean = 1 / (alpha ** 0.5) * (xt - eps_coef * eps_theta)
var = gather(self.sigma2, t)
eps = torch.randn(xt.shape, device=xt.device)
return mean + (var ** 0.5) * eps
|
参考
[1] J. Ho, A. Jain, and P. Abbeel, “Denoising Diffusion Probabilistic Models.” arXiv, Dec. 16, 2020. doi: 10.48550/arXiv.2006.11239.
代码来源:https://github.com/labmlai/annotated_deep_learning_paper_implementations/blob/master/labml_nn/diffusion/ddpm/